Diffusion Models and Gaussian Flow Matching: Two Sides of the Same Coin

Flow matching and diffusion models are two popular frameworks in generative modeling. Despite seeming similar, there is some confusion in the community about their exact connection. In this post we aim to clear up this confusion and show that diffusion models and Gaussian flow matching are the same -- Different model specifications lead to different noise schedules and loss weightings but correspond to the same generative model. That's great news, it means that you can use the two frameworks interchangeably.

Flow matching is gaining popularity recently, due to the simplicity of its formulation and the “straightness” of its induced sampling trajectories. This raises the commonly asked question:

"Which is better, diffusion or flow matching?"

As we will see, diffusion models and flow matching are equivalent (for the common special case that the source distribution used with flow matching corresponds to a Gaussian). So there is not a single answer to this question. In particular, we will show how to convert one formalism to another. Why does this equivalence matter? This allows you to mix and match techniques developed for the two frameworks. For example, after training a flow matching model, you can use either a stochastic or deterministic sampling method (in contrast to the common misunderstanding that flow matching is always deterministic).

We will focus on the most commonly used flow matching formalism , which is closely related to . Our purpose is not to downweigh the importance of either framework. In fact, both frameworks are important and derived from distinct theoretical perspectives. It is even more encouraging that they lead to the same algorithm in practice. Our goal is to help practitioners feel confident using the two frameworks interchangeably, while understanding the true degrees of freedom one has when tuning the algorithm—regardless of what it’s called.

Overview

We start with a quick overview of the two frameworks.

Diffusion models

A diffusion process gradually destroys an observed datapoint \(\bf{x}\) (such as an image) over time \(t\), by mixing the data with Gaussian noise. The noisy data at time \(t\) is given by a forward process: \(\begin{equation} {\bf z}_t = \alpha_t {\bf x} + \sigma_t {\boldsymbol \epsilon}, \;\mathrm{where} \; {\boldsymbol \epsilon} \sim \mathcal{N}(0, {\bf I}). \label{eq:forward} \end{equation}\) \(\alpha_t\) and \(\sigma_t\) define the noise schedule, such as the variance-preserving schedule, \(\alpha_t^2 + \sigma_t^2 = 1\). A useful notation is the log signal-to-noise ratio \(\lambda_t = \log(\alpha_t^2 / \sigma_t^2)\), which decreases as \(t\) increases from \(0\) (clean data) to \(1\) (Gaussian noise).

To generate new samples, we can “reverse” the forward process: We initialize the sample \({\bf z}_1\) from a standard Gaussian. Given the sample \({\bf z}_t\) at time step \(t\), we predict what the clean sample might look like with a neural network (a.k.a. denoiser model) \(\hat{\bf x} = \hat{\bf x}({\bf z}_t; t)\), and then we project it back to a lower noise level \(s\) with the same forward transformation:

\(\begin{eqnarray} {\bf z}_{s} &=& \alpha_{s} \hat{\bf x} + \sigma_{s} \hat{\boldsymbol \epsilon},\\ \end{eqnarray}\) where \(\hat{\boldsymbol \epsilon} = ({\bf z}_t - \alpha_t \hat{\bf x}) / \sigma_t\). (Alternatively we can train a neural network to predict the noise \(\hat{\boldsymbol \epsilon}\).) We keep alternating between predicting the clean data, and projecting it back to a lower noise level until we get the clean sample. This is the DDIM sampler . The randomness of samples only comes from the initial Gaussian sample, and the entire reverse process is deterministic. We will discuss the stochastic samplers later.

Flow matching

In flow Matching, the forward process is a linear interpolation between the data \({\bf x}\) and a noise term \(\boldsymbol \epsilon\): \(\begin{eqnarray} {\bf z}_t = (1-t) {\bf x} + t {\boldsymbol \epsilon}.\\ \end{eqnarray}\)

This corresponds to the diffusion forward process if the noise is Gaussian and we use the schedule \(\alpha_t = 1-t, \sigma_t = t\).

Using simple algebra, we can derive that \({\bf z}_t = {\bf z}_{s} + {\bf u} (t - s)\), where \({\bf u} = {\boldsymbol \epsilon} - {\bf x}\) is the “velocity”, “flow”, or “vector field”. Hence, to sample \({\bf z}_s\) given \({\bf z}_t\), for \(s < t\), we reverse time and replace the vector field with our best guess \(\hat{\bf u} = \hat{\bf u}({\bf z}_t; t) = \hat{\boldsymbol \epsilon} - \hat{\bf x}\), represented by a neural network, to get

\[\begin{eqnarray} {\bf z}_{s} = {\bf z}_t + \hat{\bf u}(s - t).\\ \label{eq:flow_update} \end{eqnarray}\]

Starting from the sample \({\bf z}_1\) from a standart Gaussian, we keep getting \({\bf z}_s\) at a lower noise level than \({\bf z}_t\), until we obtain the clean sample.

Comparison

So far, we can already discern the similar essences in the two frameworks:

1. Same forward process: if we assume that one end of flow matching is Gaussian, and the noise schedule of the diffusion model is in a particular form.

2. "Similar" sampling processes: both follow an iterative update that involves a guess of the clean data at the current time step. (Spoiler: below we will show they are exactly the same!)

Sampling

It is commonly thought that the two frameworks differ in how they generate samples: Flow matching sampling is deterministic with “straight” paths, while diffusion model sampling is stochastic and with “curved paths”. Below we clarify this misconception. We will focus on deterministic sampling first which is simpler; we discuss the stochastic case later on.

Imagine you want to use your trained denoiser model to transform random noise into a datapoint. Recall that the DDIM update is given by \({\bf z}_{s} = \alpha_{s} \hat{\bf x} + \sigma_{s} \hat{\boldsymbol \epsilon}\). Interestingly, rearranging terms it can be expressed in the following formulation, with respect to several network outputs and reparametrizations:

\[\begin{equation} \tilde{\bf z}_{s} = \tilde{\bf z}_{t} + \mathrm{Network \; output} \cdot (\eta_s - \eta_t) \\ \end{equation}\]

Network Output	Reparametrization
\({\bf x}\)-prediction	\(\tilde{\bf z}_t = {\bf z}_t / \sigma_t\) and \(\eta_t = {\alpha_t}/{\sigma_t}\)
\({\boldsymbol \epsilon}\)-prediction	\(\tilde{\bf z}_t = {\bf z}_t / \alpha_t\) and \(\eta_t = {\sigma_t}/{\alpha_t}\)
\({\bf u}\)-flow matching vector field	\(\tilde{\bf z}_t = {\bf z}_t/(\alpha_t + \sigma_t)\) and \(\eta_t = {\sigma_t}/(\alpha_t + \sigma_t)\)

Recall the flow matching update in Equation (4), look similar? In the last line, if we set \(\alpha_t = 1 - t\), \(\sigma_t = t\), we have \(\tilde{\bf z}_t = {\bf z}_t\) and \(\eta_t = t\), so that we recover the flow matching update! More formally, the flow matching update can be considered the Euler integration of the underlying sampling ODE (i.e.,, \(\mathrm{d}\tilde{\bf z}_t = \mathrm{[Network \; output]}\cdot\mathrm{d}\eta_t\)), and

Diffusion with DDIM sampling == Flow matching sampling (Euler).

Some other comments on the DDIM sampler:

1. The DDIM sampler analyically integrates the underlying sampling ODE if the network output is a constant over time. Of course the network prediction is not constant, but it means the inaccuracy of DDIM sampler only comes from approximating the intractable integral of the network output (not from additional linear term of ${\bf z}_t$ as in the Euler sampler of probability flow ODE ). This holds for all three network outputs.

2. The DDIM update and final samples are invariant to a linear scaling applied to the noise schedule, as a scaling does not affect $\tilde{\bf z}_t$ and $\eta_t$.

To validate Claim 2, we present the results obtained using several noise schedules, each of which follows a flow-matching schedule with different scaling factors. At the left end, the scaling factor is \(1\) which is exactly the flow matching schedule, while at the right end, the scaling factor is \(1/[(1-t)^2 + t^2]\), which corresponds to a variance-preserving schedule (Feel free to change the slider). We see that DDIM (and flow matching sampler) always gives the same final samples, regardless of the scaling of the schedule. The paths bend in different ways as \({\bf z}_t\) (but not \(\tilde{\bf z}_t\)) is scale-dependent along the path. For the Euler sampler applied to the diffusion probabilty flow ODE introduced in , the scaling makes a true difference: we see that both the paths and the final samples change.

Wait a second? It is often said that the flow matching results in straight paths, but in the above figure its sampling trajectories look curved.

So why is flow matching said to result in straight sampling paths? If the model would be perfectly confident about the data point it is moving to, the path from noise to data will be a straight line with the flow matching schedule. Straight line ODEs would be great because it means that there is no integration error whatsoever. Unfortunately, the predictions are not for a single point. Instead they average over a larger distribution. And flowing straight to a point != straight to a distribution.

In the interactive graph below, you can change the variance of the data distribution on the right hand side by the slider. Note how the variance preserving schedule is better (straighter paths) for wide distributions, while the flow matching schedule works better for narrow distributions.

Finding such straight paths for real-life datasets like images is of course much less straightforward. But the conclusion remains the same: The optimal integration method depends on the data distribution.

Two important takeaways from deterministic sampling:

1. DDIM is equivalent to the flow matching sampling, and is invariant to a linear scaling to the noise schedule.

2. Flow matching schedule is only straight for a model predicting a single point. For realistic distributions other interpolations can give straighter paths.

Training

Diffusion models are trained by estimating \(\hat{\bf x} = \hat{\bf x}({\bf z}_t; t)\), or alternatively \(\hat{\boldsymbol \epsilon} = \hat{\boldsymbol \epsilon}({\bf z}_t; t)\) with a neural net. Learning the model is done by minimizing a weighted mean squared error (MSE) loss: \(\begin{equation} \mathcal{L}(\mathbf{x}) = \mathbb{E}_{t \sim \mathcal{U}(0,1), \boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})} \left[ \textcolor{green}{w(\lambda_t)} \cdot \frac{\mathrm{d}\lambda}{\mathrm{d}t} \cdot \lVert\hat{\boldsymbol \epsilon} - {\boldsymbol \epsilon}\rVert_2^2 \right], \end{equation}\) where \(\lambda_t\) is the log signal-to-noise ratio, and \(\textcolor{green}{w(\lambda_t)}\) is the weighting function, balancing the importance of the loss at different noise levels. The term \(\mathrm{d}\lambda / {\mathrm{d}t}\) in the training objective seems unnatural and in the literature is often merged with the weighting function. However, their separation helps disentangle the factors of noise schedule and weighting function clearly, and helps emphasize the more design choice: the weighting function.

Flow matching also fits in the above training objective. Recall below is the conditional flow matching objective used by :

\[\begin{equation} \mathcal{L}_{\mathrm{CFM}}(\mathbf{x}) = \mathbb{E}_{t \sim \mathcal{U}(0,1), \boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})} \left[ \lVert \hat{\bf u} - {\bf u} \rVert_2^2 \right] \end{equation}\]

Since \(\hat{\bf u}\) is a linear combination of \(\hat{\boldsymbol \epsilon}\) and \({\bf z}_t\), the CFM training objective can be rewritten as mean squared error on \({\boldsymbol \epsilon}\) with a specific weighting.

How do we choose what the network should output?

Below we summarize several network outputs proposed in the literature, including a few versions used by diffusion models and the one used by flow matching. They can be derived from each other given the current data \({\bf z}_t\). One may see the training objective defined with different network outputs in different papers. From the perspective of training objective, they all correspond to having some additional weighting in front of the \({\boldsymbol \epsilon}\)-MSE that can be absorbed in the weighting function.

Network Output	Formulation	MSE on Network Output
\({\boldsymbol \epsilon}\)-prediction	\(\hat{\boldsymbol \epsilon}\)	\(\lVert\hat{\boldsymbol{\epsilon}} - \boldsymbol{\epsilon}\rVert_2^2\)
\({\bf x}\)-prediction	\(\hat{\bf x} = ({\bf x}_t - \sigma_t \hat{\boldsymbol \epsilon}) / \alpha_t\)	\(\lVert\hat{\bf x} - {\bf x}\rVert_2^2 = e^{-\lambda} \lVert\hat{\boldsymbol \epsilon} - {\boldsymbol \epsilon}\rVert_2^2\)
\({\bf v}\)-prediction	\(\hat{\bf v} = \alpha_t \hat{\boldsymbol{\epsilon}} - \sigma_t \hat{\bf x}\)	\(\lVert\hat{\bf v} - {\bf v}\rVert_2^2 = \alpha_t^2(e^{-\lambda} + 1)^2 \lVert\hat{\boldsymbol \epsilon} - {\boldsymbol \epsilon}\rVert_2^2\)
\({\bf u}\)-flow matching vector field	\(\hat{\bf u} = \hat{\boldsymbol{\epsilon}} - \hat{\bf x}\)	\(\lVert\hat{\bf u} - {\bf u}\rVert_2^2 = (e^{-\lambda / 2} + 1)^2 \lVert\hat{\boldsymbol \epsilon} - {\boldsymbol \epsilon}\rVert_2^2\)

In practice, however, the model output might make a difference. For example,

• \({\boldsymbol \epsilon}\)-prediction can be problematic at high noise levels, because any error in \(\hat{\boldsymbol \epsilon}\) will get amplified in \(\hat{\bf x} = ({\bf x}_t - \sigma_t \hat{\boldsymbol \epsilon}) / \alpha_t\), as \(\alpha_t\) is close to 0. It means that small changes create a large loss under some weightings.

• Following the similar reason, \({\bf x}\)-prediction is problematic at low noise levels, because \(\hat{\bf x}\) is not informative, and the error gets amplified in \(\hat{\boldsymbol \epsilon}\).

Therefore, a heuristic is to choose a network output that is a combination of \({\bf x}\)- and \({\boldsymbol \epsilon}\)-predictions, which applies to the \({\bf v}\)-prediction and the flow matching vector field \({\bf u}\).

How do we choose the weighting term?

The weighting is the most important part of the loss, it balances the importance of high frequency and low frequency components . This is important when modeling images, videos and audio, as certain high frequency components in those signals are not perceptible to humans, and thus it is better not to waste model capacity on them. Viewing losses via their weighting, one can derive that:

Flow matching weighting == diffusion weighting of ${\bf v}$-MSE loss + cosine noise schedule.

That is, the flow matching training objective is the same as a commonly used setting in diffusion models! See Appendix D.2-3 in for a detailed derivation. Below we plot several commonly used weighting functions in the literature, as a function of \(\lambda\).

The flow matching weighting (also \({\bf v}\)-MSE weighting) decreases exponentially as \(\lambda\) increases. Empirically we find another interesting connection: The stable diffusion 3 weighting, a reweighted version of flow matching, is very similar to the EDM weighting that is popular for diffusion models.

How do we choose the noise schedule?

A few remarks about training noise schedule:

1. All noise schedules can be normalized as a variance-preserving schedule, with a linear scaling of \({\bf z}_t\) and an unscaling at the network input. The key defining property of a noise schedule is the log signal-to-noise ratio \(\lambda_t\).
2. The training loss is invariant to the training noise schedule, since the loss fuction can be rewritten as \(\mathcal{L}(\mathbf{x}) = \int_{\lambda_{\min}}^{\lambda_{\max}} w(\lambda) \mathbb{E}_{\boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})} \left[ \|\hat{\boldsymbol{\epsilon}} - \boldsymbol{\epsilon}\|_2^2 \right] \, d\lambda\), which is only related to the endpoints but not the schedule of \(\lambda_t\). However, \(\lambda_t\) might still affect the variance of the Monte Carlo estimator of the training loss. A few heuristics have been proposed in the literature to automatically adjust the noise schedules over the course of training. This blog post has a nice summary.
3. One can choose completely different noise schedules for training and sampling, based on distinct heuristics: For training, it is desirable to have a noise schedule that minimizes the variance of the Monte Calor estimator, whereas for sampling the noise schedule is more related to the discretization error of the ODE / SDE sampling trajectories and the model curvature.

Summary

In summary, we have the following conclusions for diffusion models / flow matching training:

1. Weighting function is important for training. For perceptual signals, it balances the importance of different frequency components. It should be tuned based on data characteristics.

2. Noise schedule is far less important to the training objective but affects the training efficiency.

3. The network output proposed by flow matching nicely balances ${\bf x}$- and ${\epsilon}$-prediction, similar to ${\bf v}$-prediction.

Diving deeper into samplers

In this section, we discuss different kinds of samplers in more detail.

Reflow operator

The Reflow operation in Flow Matching connects noise and data points in a straight line. One can obtain these (data, noise) pairs by running a deterministic sampler from noise. A model can then be trained to directly predict the data given the noise avoiding the need for sampling. In the diffusion literature the same approach was the one of the first distillation techniques .

Deterministic sampler vs. stochastic sampler

So far we have just discussed the deterministic sampler of diffusion models or flow matching. An alternative is to use stochastic samplers such as the DDPM sampler .

Performing one DDPM sampling step going from $\lambda_t$ to $\lambda_t + \Delta\lambda$ is exactly equivalent to performing one DDIM sampling step to $\lambda_t + 2\Delta\lambda$, and then renoising to $\lambda_t + \Delta\lambda$ by doing forward diffusion. The renoising by doing forward diffusion thus reverses exactly half the progress made by DDIM. To see this, let’s take a look at a 2D example. Starting from the same mixture of Gaussians distribution, we either perform a DDIM sampling step but reverse the sign of the update, or a forward diffusion step:

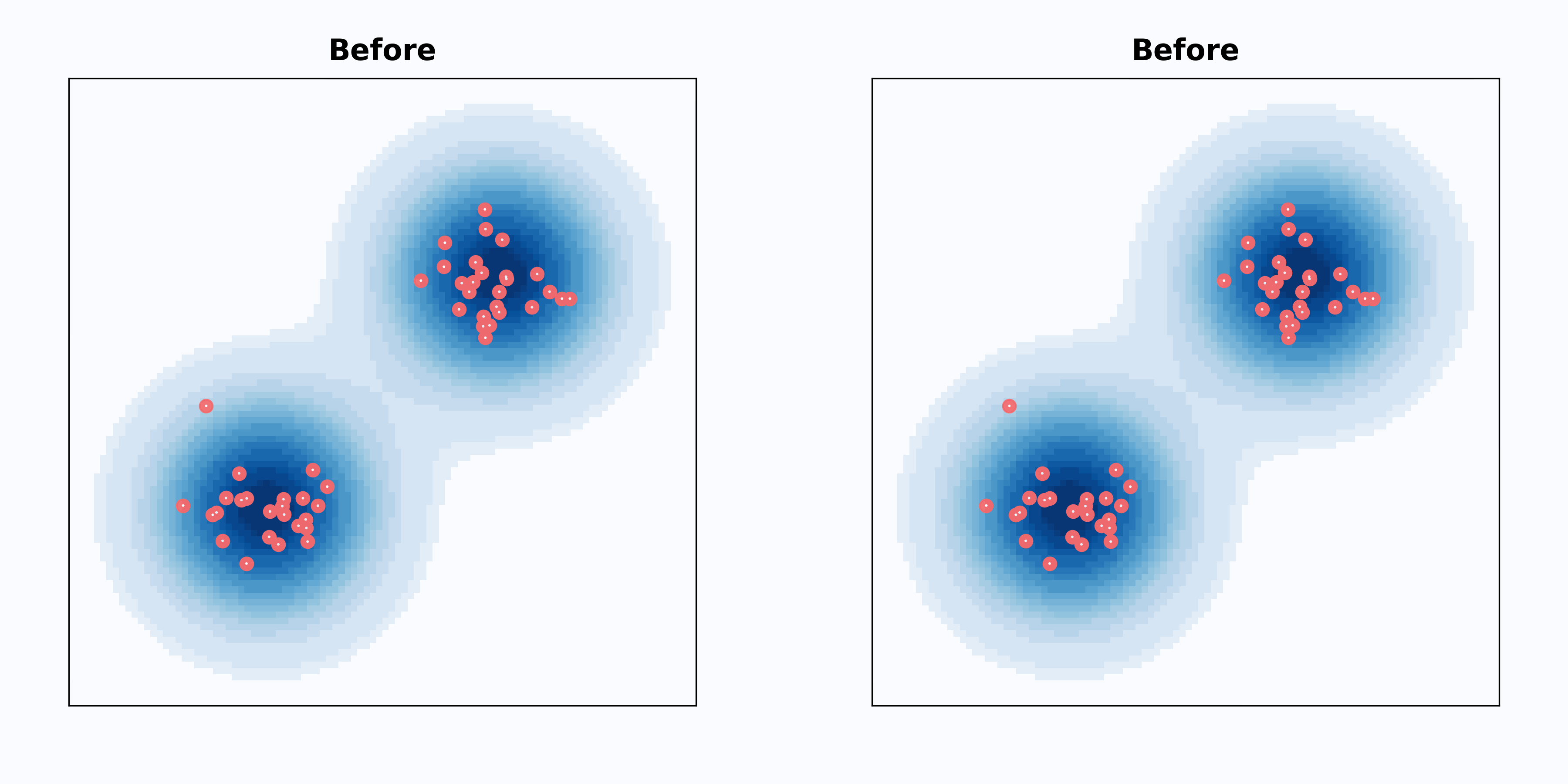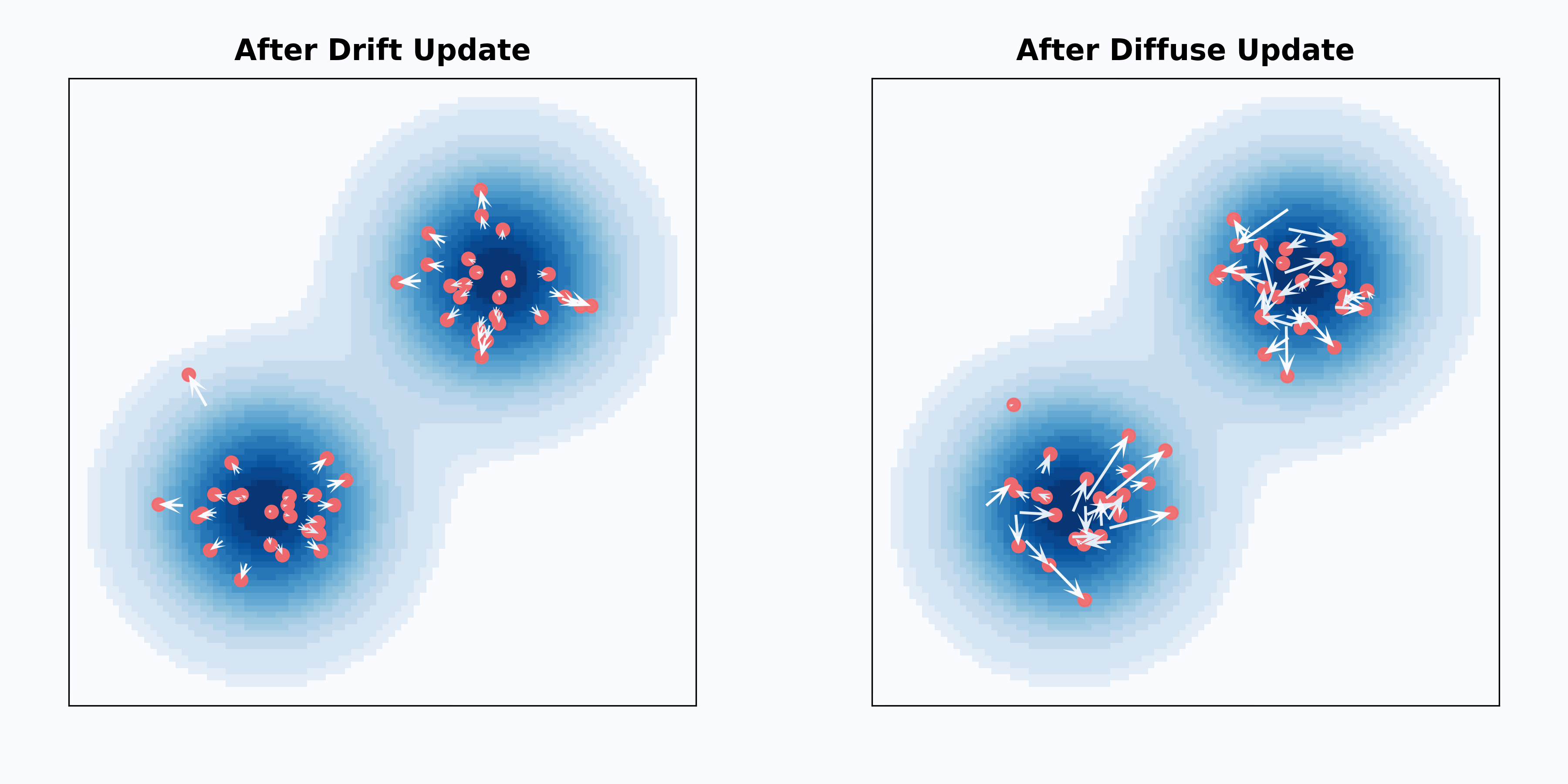
For each individual sample, the two updates are very different: The reverse DDIM update consistently drags every sample away from the modes of the distribution, while the diffusion update is purely random. However, aggregating all samples together, the distributions after the updates are the same. Therefore if we perform the same DDIM sampling step (without reversing the sign of the update), followed by the forward diffusion step, the distribution will remain the same as the one before the two updates.

The fraction of the DDIM step to undo by renoising is a hyperparameter which we are free to choose (doesn’t have to be , and which has been called the level of churn by . The effect of adding churn to our sampler is to diminish the effect on our final sample of our model predictions made early during sampling, and to increase the weight on later predictions. This is shown in the figure below

Here we ran different samplers for 100 sampling steps using a cosine noise schedule

and \({\bf v}\)-prediction . Ignoring nonlinear interactions, the final sample produced by the sampler can be written as a weighted sum of predictions \(\hat{\bf v}_t\) made during sampling and Gaussian noise \({\bf e}\): \({\bf z}_0 = \sum_t h_t \hat{\bf v}_t + c {\bf e}\). The weights \(h_t\) of these predictions are shown on the y-axis for different diffusion times \(t\) shown on the x-axis. DDIM results in an equal weighting of \({\bf v}\)-predictions for this setting, as shown ,

whereas DDPM puts more emphasis on predictions made towards the end of sampling. Also see for analytic expressions of these weights in the \({\bf x}\) and \({\boldsymbol \epsilon}\) parameterizations.

SDE and ODE Perspective

We’ve observed the practical equivalence between diffusion models and flow matching algorithms. Here, we formally describe the equivalence of the forward process and sampling using ODE and SDE, as a completeness in theory and closing chapter.

Diffusion Model

The forward process of diffusion models which gradually destroys a data over time can be described by the following stochastic differential equation (SDE):

\[\begin{equation} \mathrm{d} {\bf z}_t = f_t {\bf z}_t \mathrm{d} t + g_t \mathrm{d} {\bf z} , \end{equation}\]

where \(\mathrm{d} {\bf z}\) is an infinitesimal Gaussian (formally, a Brownian motion). $f_t$ and $g_t$ decide the noise schedule. The generative process is given by the reverse of the forward process, whose formula is given by

\[\begin{equation} \mathrm{d} {\bf z}_t = \left( f_t {\bf z}_t - \frac{1+ \eta_t^2}{2}g_t^2 \nabla \log p_t({\bf z_t}) \right) \mathrm{d} t + \eta_t g_t \mathrm{d} {\bf z} , \end{equation}\]

where $\nabla \log p_t$ is the score of the forward process.

Note that we have introduced an additional parameter $\eta_t$ which controls the amount of stochasticity at inference time. This is related to the churn parameter introduced before. When discretizing the backward process we recover DDIM in the case $\eta_t = 0$ and DDPM in the case $\eta_t = 1$.

Flow Matching

The interpolation between \({\bf x}\) and \({\boldsymbol \epsilon}\) in flow matching can be described by the following ordinary differential equation (ODE):

\[\begin{equation} \mathrm{d}{\bf z}_t = {\bf u}_t \mathrm{d}t. \end{equation}\]

Assuming the interpolation is \({\bf z}_t = \alpha_t {\bf x} + \sigma_t {\boldsymbol \epsilon}\), then \({\bf u}_t = \dot{\alpha}_t {\bf x} + \dot{\sigma}_t {\boldsymbol \epsilon}\).

The generative process is simply reverse the ODE in time. This is a specific case of stochastic interpolation, in which case it can be generalized to an SDE:

\(\begin{equation} \mathrm{d} {\bf z}_t = ({\bf u}_t - \frac{1}{2} \varepsilon_t^2 \nabla \log p_t({\bf z_t})) \mathrm{d} t + \varepsilon_t \mathrm{d} {\bf z}, \end{equation}\) where \(\varepsilon_t\) controls the amount of stochasticity at inference time.

Equivalence of the two frameworks

To summary, both frameworks are defined by three hyperparameters respectively: $f_t, g_t, \eta_t$ for diffusion, and $\alpha_t, \sigma_t, \varepsilon_t$ for flow matching. We can show the equivalence by deriving one set of hyperparameters from the other. From diffusion to flow matching:

\[\alpha_t = \exp\left(\int_0^t f_s \mathrm{d}s\right) , \quad \sigma_t = \left(\int_0^t g_s^2 \exp\left(-2\int_0^s f_u \mathrm{d}u\right) \mathrm{d} s\right)^{1/2} , \quad \varepsilon_t = \eta_t g_t .\]

From flow matching to diffusion:

\[f_t = \partial_t \log(\alpha_t) , \quad g_t = 2 \alpha_t \sigma_t \partial_t (\sigma_t / \alpha_t) , \quad \eta_t = \varepsilon_t / (2 \alpha_t \sigma_t \partial_t (\sigma_t / \alpha_t)) .\]

In summary, aside from training considerations and sampler selection, diffusion and Gaussian flow matching exhibit no fundamental differences.

Closing thoughts

If you’ve read this far, we hope we’ve convinced you that diffusion models and Gaussian flow matching are equivalent. When developing your own codebase or techniques, there’s no need to implement them separately under these two “distinct” frameworks. Similarly, if you’re working on one method, it’s likely unnecessary to reframe it within the context of the other. The key is to focus on the design choices that truly matter. With this equivalence in mind, improvements made to specific design choices in one framework will naturally benefit the other. We hope this perspective helps practitioners have more fun playing with these models, while fostering deeper connections between works in the literature.