Flow With What You Know
We provide an accessible introduction to flow-matching and rectified flow models, which are increasingly at the forefront of generative AI applications. Typical descriptions of them are often laden with extensive probability-math equations, which can form barriers to the dissemination and understanding of these models. Fortunately, before they were couched in probabilities, the mechanisms underlying these models were grounded in basic physics, which provides an alternative and highly accessible (yet functionally equivalent) representation of the processes involved.
Introduction
Flow-based generative AI models
Intuitively, these models operate akin to the fluid processes that transform the shapes of clouds in the sky. While recent expositions
What’s a Flow?
In the real world, things typically follow curved paths - like water flowing in a river, or crowds of people navigating around obstacles. Here’s map of wind provided from the WW2010 atmospheric science project at UIUC: at every point in space, the wind has a velocity vector, and the air moves along “streamlines” or “trajectories” parallel to the velocity vectors…
Source: atmos.uiuc.edu
Notice that the streamlines never cross. If the streams were to cross… “it would be bad.”
So, at every point in space there’s a velocity vector telling the little bits of fluid where to go. And just like water or wind flows may depend not only on spatial position but also time, so too can our velocity vector field depend on position and time.
Flow matching learns these natural paths by focusing on the velocity at each point - essentially asking, “Which way should each data point be moving at this moment?”
It may seem confusing to see "flow matching" and "rectified flows" sometimes used interchangeably, but this is because they are the same
Also, note that there is no explicit "rectification" mechanism in rectified flows; rather, "rectified" is a description of the effect of flow-matching, i.e., of transforming crossing trajectories to non-crossing ones. The addition of "Reflow" to the rectified flow paper
How Do FM/RF Models Work?
To gain a deep understanding of how models work, having an executable toy model is often a key instructional tool. This tutorial is written as an executable Jupyter notebook
For instance, the code starts with importing packages…
Show code: Installs & imports
# Uncomment to install any missing dependencies:
#%pip install torch numpy matplotlib tqdm plotly
import torch
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from IPython.display import HTML, display, clear_output
from tqdm.notebook import tqdm
import plotly.graph_objects as goChoose Your Own Data Shapes
The executable notebook verison of this lesson lets you choose various shapes to “morph” between. For this reading, we’ll go from a Gaussian to a Spiral, but other choices are available in the notebook.
# Options are: 'Gaussian', 'Square', 'Heart', 'Spiral','Two Gaussians', 'Smiley'
source_data_choice = 'Gaussian'
target_data_choice = 'Spiral' With the imports in place and the choice of starting and ending distributions made, we’re ready to define some utilities to generate and visualize our data. Let’s take a look:
Show code: Utilities, styles, functions, generators, visualization
# for accessibility: Wong's color pallette: cf. https://davidmathlogic.com/colorblind
#wong_black = [0/255, 0/255, 0/255] # #000000
wong_amber = [230/255, 159/255, 0/255] # #E69F00
wong_cyan = [86/255, 180/255, 233/255] # #56B4E9
wong_green = [0/255, 158/255, 115/255] # #009E73
wong_yellow = [240/255, 228/255, 66/255] # #F0E442
wong_navy = [0/255, 114/255, 178/255] # #0072B2
wong_red = [213/255, 94/255, 0/255] # #D55E00
wong_pink = [204/255, 121/255, 167/255] # #CC79A7
wong_cmap = [wong_amber, wong_cyan, wong_green, wong_yellow, wong_navy, wong_red, wong_pink]
source_color = wong_navy
target_color = wong_red
pred_color = wong_green
line_color = wong_yellow
bg_theme = 'dark' # 'black', 'white', 'dark', 'light'
if bg_theme in ['black','dark']:
plt.style.use('dark_background')
else:
plt.rcdefaults()
# A few different data distributions
def create_gaussian_data(n_points=1000, scale=1.0):
"""Create a 2D Gaussian distribution"""
return torch.randn(n_points, 2) * scale
def create_square_data(n_points=1000, scale=3.0): # 3 is set by the spread of the gaussian and spiral
"""Create points uniformly distributed in a square"""
# Generate uniform points in a square
points = (torch.rand(n_points, 2) * 2 - 1) * scale
return points
def create_spiral_data(n_points=1000, scale=1):
"""Create a spiral distribution. i like this one more"""
noise = 0.1*scale
#theta = torch.linspace(0, 6*np.pi, n_points) # preferred order? no way
theta = 6*np.pi* torch.rand(n_points)
r = theta / (2*np.pi) * scale
x = r * torch.cos(theta) + noise * torch.randn(n_points)
y = r * torch.sin(theta) + noise * torch.randn(n_points)
return torch.stack([x, y], dim=1)
def create_heart_data(n_points=1000, scale=3.0):
"""Create a heart-shaped distribution of points"""
square_points = create_square_data(n_points, scale=1.0)
# Calculate the heart-shaped condition for each point
x, y = square_points[:, 0], square_points[:, 1]
heart_condition = x**2 + ((5 * (y + 0.25) / 4) - torch.sqrt(torch.abs(x)))**2 <= 1
# Filter out points that don't satisfy the heart-shaped condition
heart_points = square_points[heart_condition]
# If we don't have enough points, generate more
while len(heart_points) < n_points:
new_points = create_square_data(n_points - len(heart_points), scale=1)
x, y = new_points[:, 0], new_points[:, 1]
new_heart_condition = x**2 + ((5 * (y + 0.25) / 4) - torch.sqrt(torch.abs(x)))**2 <= 1
new_heart_points = new_points[new_heart_condition]
heart_points = torch.cat([heart_points, new_heart_points], dim=0)
heart_points *= scale
return heart_points[:n_points]
def create_two_gaussians_data(n_points=1000, scale=1.0, shift=2.5):
"""Create a 2D Gaussian distribution"""
g = torch.randn(n_points, 2) * scale
g[:n_points//2,0] -= shift
g[n_points//2:,0] += shift
indices = torch.randperm(n_points)
return g[indices]
def create_smiley_data(n_points=1000, scale=2.5):
"make a smiley face"
points = []
# Face circle
#angles = 2 * np.pi * torch.rand(n_points//2+20)
#r = scale + (scale/10)*torch.sqrt(torch.rand(n_points//2+20))
#points.append(torch.stack([r * torch.cos(angles), r * torch.sin(angles)], dim=1))
# Eyes (small circles at fixed positions)
for eye_pos in [[-1, 0.9], [1, 0.9]]:
eye = torch.randn(n_points//3+20, 2) * 0.2 + torch.tensor(eye_pos) * scale * 0.4
points.append(eye)
# Smile (arc in polar coordinates)
theta = -np.pi/6 - 2*np.pi/3*torch.rand(n_points//3+20)
r_smile = scale * 0.6 + (scale/4)* torch.rand_like(theta)
points.append(torch.stack([r_smile * torch.cos(theta), r_smile * torch.sin(theta)], dim=1))
points = torch.cat(points, dim=0) # concatenate first
points = points[torch.randperm(points.shape[0])] # then shuffle
return points[:n_points,:]
# Initialize generator functions
source_gen_fn = None
target_gen_fn = None
# Assign generator functions based on user choices
for gen_choice, gen_fn_name in zip([source_data_choice, target_data_choice], ['source_gen_fn', 'target_gen_fn']):
gen_choice = gen_choice.lower()
if 'two gaussians' in gen_choice:
gen_fn = create_two_gaussians_data
elif 'heart' in gen_choice:
gen_fn = create_heart_data
elif 'spiral' in gen_choice:
gen_fn = create_spiral_data
elif 'square' in gen_choice:
gen_fn = create_square_data
elif 'smiley' in gen_choice:
gen_fn = create_smiley_data
else:
gen_fn = create_gaussian_data
if gen_fn_name == 'source_gen_fn':
source_gen_fn = gen_fn
else:
target_gen_fn = gen_fn
# A couple aliases so we can easily switch distributions without affecting later code
def create_source_data(n_points=1000, hshift=0): # hshift can make it a bit easier to see trajectories later
g = source_gen_fn(n_points=n_points)
if hshift != 0: g[:,0] += hshift
return g
def create_target_data(n_points=1000, hshift=0):
g = target_gen_fn(n_points=n_points)
if hshift != 0: g[:,0] += hshift
return g
def plot_distributions(dist1, dist2, title1="Distribution 1", title2="Distribution 2", alpha=0.8):
"""Plot two distributions side by side"""
plt.close('all')
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
ax1.scatter(dist1[:, 0], dist1[:, 1], alpha=alpha, s=10, color=source_color)
ax2.scatter(dist2[:, 0], dist2[:, 1], alpha=alpha, s=10, color=target_color)
ax1.set_title(title1)
ax2.set_title(title2)
# Set same scale for both plots
max_range = max(
abs(dist1).max().item(),
abs(dist2).max().item()
)
for ax in [ax1, ax2]:
ax.set_xlim(-max_range, max_range)
ax.set_ylim(-max_range, max_range)
ax.set_aspect('equal')
plt.tight_layout()
plt.show() # Explicitly show the plot
plt.close()
def interpolate_color(t, start='blue', end='red'):
"""Interpolate from matplotlib's default green (t=0) to red (t=1)"""
start_color = plt.cm.colors.to_rgb(start)
end_color = plt.cm.colors.to_rgb(end)
return (1-t) * np.array(start_color) + t * np.array(end_color)
def show_flow_sequence(start_dist, end_dist, n_steps=5, c_start=source_color, c_end=target_color):
"""Show the flow as a sequence of static plots"""
fig, axes = plt.subplots(1, n_steps, figsize=(4*n_steps, 4))
max_range = max(
abs(start_dist).max().item(),
abs(end_dist).max().item()
)
for i, ax in enumerate(axes):
t = i / (n_steps - 1)
current = start_dist * (1-t) + end_dist * t
color = interpolate_color(t, start=c_start, end=c_end)
ax.scatter(current[:, 0], current[:, 1],
alpha=0.8, s=10,
c=[color])
ax.set_xlim(-max_range, max_range)
ax.set_ylim(-max_range, max_range)
ax.set_aspect('equal')
ax.set_title(f't = {t:.2f}')
plt.tight_layout()
plt.show()
plt.close()
# Create our distributions and look at them
n_points = 1000
source, target = create_source_data(n_points), create_target_data(n_points)
plot_distributions(source, target, "Starting Distribution", "Target Distribution")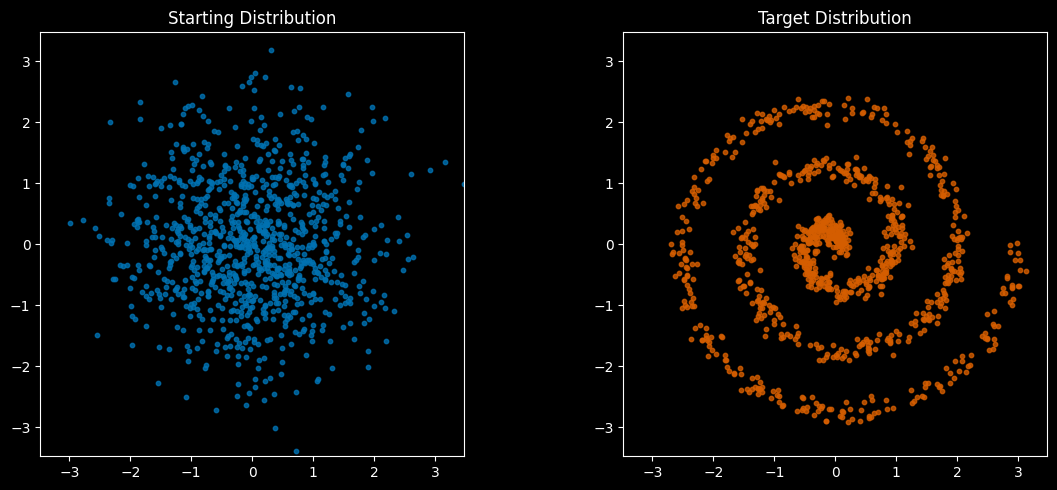
The process of transitioning from the starting “source” to the final “target” might include snapshots like these:

(Note the colors aren’t meaningful, they’re just added to make it easier to distinguish what we’re looking at. Our data are just points in 2-D space.)
So, how do we get the points from the source distribution to fit with the target distribution? The simplest way (though not the only way) is to assume points move in straight lines from source to target. Even though our network might learn more complex paths later, this gives us a starting point for training.
The Starting Setup
The training setup for flow matching models is as follows:
- We start by randomly pairing points from the source & the target – yes, really. 🤣
- We move the points along straight trajectories, and the speed of each point is constant.
Show code: Make 2D flow-matching diagram with crossing lines
source_L = source.clone()
shift = 5
source_L[:,0] -= shift
target_R = target.clone()
target_R[:,0] += shift # Note: fixed the indexing here from [:0] to [:,0]
fig, ax = plt.subplots(figsize=(8,4))
# show the whole distribution
ax.scatter(source_L[:,0], source_L[:,1], color=source_color, alpha=0.5)
ax.scatter(target_R[:,0], target_R[:,1], color=target_color, alpha=0.5)
# Draw lines connecting points, with source & target points outlined
n_lines = 15
ax.scatter(source_L[:n_lines,0], source_L[:n_lines,1], color=source_color, alpha=0.5,
facecolor='none', edgecolor=line_color,)
ax.scatter(target_R[:n_lines,0], target_R[:n_lines,1], color=target_color, alpha=0.5,
facecolor='none', edgecolor=line_color,)
for i in range(n_lines):
ax.plot([source_L[i,0], target_R[i,0]],
[source_L[i,1], target_R[i,1]],
'-', alpha=0.3, color=line_color+[.9],
linewidth=2) # or lw=2
ax.set_aspect('equal')
ax.set_xticks([])
ax.set_yticks([])
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['left'].set_visible(False)
for [x, label] in zip([-shift,shift], ['Source','Target']):
ax.text(x, 4, label, fontsize=12, color='black', ha='center', va='center',)
plt.show()
plt.close()
The idea of trying straight trajectories at constant speed is *identical* to simple linear interpolation between source and target data points.
There are big issues with doing this: The random pairing results in lots of trajectories that cross each other. But this is a starting point for Flow Matching.
…well, ok not quite: we’re going to allow the trajectories of individual points to cross as we train the model. This is a bit “confusing” for the model, which will be trying to learn a velocity field, and that isn’t defined where trajectories cross. Eventually, however, the model will learn to estimate the aggregated motion of many particles, which will sort of average out to arrive at the “bulk motion” of the flow. This is similar to how the Brownian motion
This is why flow matching is about transforming distributions, not individual points. The learned velocity field might not exactly match any of our training trajectories, but it captures the statistical flow needed to transform one distribution into another.
Here’s a visualization from the code we’ll execute later in the lesson. We’ll plot…
- Our naive training trajectories (with crossings)
- The actual learned flow field (i.e., the velocity vector field)
- The paths (aka “trajectories”) that data points follow when flowing with the learned field

Left: Training data uses simple straight lines (with many crossings). Middle: The learned flow (velocity vector) field is smooth and continuous. Right: Actual trajectories following the flow field don’t cross.
How Are Flows “Learned”?
The goal of the machine learning system is as follows: for any point in space and any time t between 0 and 1, we want to learn the correct velocity (direction and speed) that point should move. It’s like learning the “wind map” that will blow the starting distribution cloud into the shape of the target distribution cloud.
Since neural networks are such useful engines for approximation and interpolation, we’ll let a neural network “learn” to estimate the mapping between locations and times (as inputs), and velocities (as outputs).
You'll sometimes see flow-maching models being referred to as "simulation free." This is just an indication that the flow we arrive at is not the result of any explicit simulation of any process (physical or otherwise). The flow obtained arises simply from the aggregation (or "averaging out") of many particles moving along imagined straight lines and crossing paths.
The Neural Network’s Job
The neural network has one job: given a position in space and a time, to output a velocity vector. That’s all it does. Below is the code for this model that will “learn” to estimate velocity vectors.
import torch.nn as nn
import torch.nn.functional as F
class VelocityNet(nn.Module):
def __init__(self, input_dim, h_dim=64):
super().__init__()
self.fc_in = nn.Linear(input_dim + 1, h_dim)
self.fc2 = nn.Linear(h_dim, h_dim)
self.fc3 = nn.Linear(h_dim, h_dim)
self.fc_out = nn.Linear(h_dim, input_dim)
def forward(self, x, t, act=F.gelu):
t = t.expand(x.size(0), 1) # Ensure t has the correct dimensions
x = torch.cat([x, t], dim=1)
x = act(self.fc_in(x))
x = act(self.fc2(x))
x = act(self.fc3(x))
return self.fc_out(x)
# Instantiate the model
input_dim = 2
model = VelocityNet(input_dim)…That’s it! Looks pretty simple, right? That’s because to make the system work we’ll need more than just the velocity field model.
Apart from the velocity model (i.e., the neural network, for us), the rest of the software system then uses these generated velocities to move points around. The model’s velocities are then used in a differential equation describing the small change to each particle’s position $\vec{r}$ over a short time $dt$:
\[d\vec{r} = \vec{v}(\vec{r},t) dt\]That equation is integrated by some (totally separate) numerical integration routine. A popular choice in the machine learning world is the “forward Euler” method, which is simple to implement, but will need to be upgraded (see further below) to get good results.
Show code: Integrator to generate/predict samples using the trained model
@torch.no_grad()
def fwd_euler_step(model, current_points, current_t, dt):
velocity = model(current_points, current_t)
return current_points + velocity * dt
@torch.no_grad()
def integrate_path(model, initial_points, step_fn=fwd_euler_step, n_steps=100,
save_trajectories=False, warp_fn=None):
"""this 'sampling' routine is primarily used for visualization."""
device = next(model.parameters()).device
current_points = initial_points.clone()
ts = torch.linspace(0,1,n_steps).to(device)
if warp_fn: ts = warp_fn(ts)
if save_trajectories: trajectories = [current_points]
for i in range(len(ts)-1):
current_points = step_fn(model, current_points, ts[i], ts[i+1]-ts[i])
if save_trajectories: trajectories.append(current_points)
if save_trajectories: return current_points, torch.stack(trajectories).cpu()
return current_points
generate_samples = integrate_path # just lil' alias for the probability / diffusion model crowd ;-) Training Code
The goal of the training code is twofold:
- to expose the model to as many locations and times as possible – at least for those times & locations that “matter most”. This exposure is what I’ll refer to as “coverage”.
- to force the model to learn to generate (approximately) correct velocities at those times and locations.
That’s it. The training code doesn’t actually do any integration or “solving,” but we’ll typically execute the integration on some validation data during training just to visualize “how we’re doing” as the training progresses.
Show code: viz routine calls integrator, makes pictures
#| code-fold: true
#| code-summary: "Viz code: calls integrator to calc motion given v field, makes pictures"
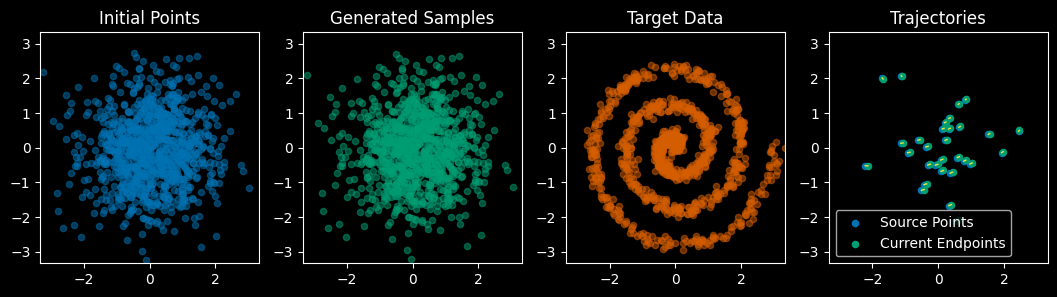
def viz(val_points, target_samples, trained_model, size=20, alpha=0.5, n_steps=100, warp_fn=None,):
# Generate and visualize new samples
device = next(trained_model.parameters()).device
generated_samples, trajectories = integrate_path(trained_model, val_points.to(device), n_steps=n_steps, warp_fn=warp_fn, save_trajectories=True)
n_viz = min(30, len(trajectories[0])) # Number of trajectories to visualize
fig, ax = plt.subplots(1,4, figsize=(13,3))
data_list = [val_points.cpu(), generated_samples.cpu(), target_samples.cpu()]
label_list = ['Initial Points', 'Generated Samples', 'Target Data','Trajectories']
color_list = [source_color, pred_color, target_color]
global_max = max( torch.max(torch.abs(torch.cat(data_list)),0)[0][0], torch.max(torch.abs(torch.cat(data_list)),0)[0][1] )
for i in range(len(label_list)):
ax[i].set_title(label_list[i])
ax[i].set_xlim([-global_max, global_max])
ax[i].set_ylim([-global_max, global_max])
if i < 3: # non-trajectory plots
ax[i].scatter( data_list[i][:, 0], data_list[i][:, 1], s=size, alpha=alpha,
label=label_list[i], color=color_list[i])
else:
# Plot trajectory paths first
for j in range(n_viz):
path = trajectories[:, j]
ax[3].plot(path[:, 0], path[:, 1], '-', color=line_color, alpha=1, linewidth=1)
# Then plot start and end points for the SAME trajectories
start_points = trajectories[0, :n_viz]
end_points = trajectories[-1, :n_viz]
ax[3].scatter(start_points[:, 0], start_points[:, 1], color=source_color, s=size, alpha=1, label='Source Points')
ax[3].scatter(end_points[:, 0], end_points[:, 1], color=pred_color, s=size, alpha=1, label='Current Endpoints')
ax[3].legend()
plt.show()
plt.close()
# Visualize the data
n_samples = 1000
source_samples = create_source_data(n_samples)
target_samples = create_target_data(n_samples)
val_points = create_source_data(n_samples)
print("Testing visualization routines (before training):")
viz(val_points, target_samples, model) Testing visualization routines (before training):
The clever part about flow matching is how we train this network. For each training step:
- Sample random points from our source and target distributions, and pair the points
- Sample random times between 0 and 1
- Calculate the locations where these points would be at those times if they were moving at constant velocity from source to target locations
- Calculate what velocity they would have at those locations if they were moving at constant velocity
- Train the network to predict these velocities – which will end up “seeking the mean” when the network has to do the same for many, many points.
Some readers may be skeptical: “Could such a scheme even work?” Theoretical assurances to that effect are where the pages probability-math come in. However, machine learning is also an experimental science, as in “Try it and find out!”
Here we run the training code…
Show code: train_model() training loop
#| code-fold: true
#| code-summary: "Code for train_model() training loop"
import torch.optim as optim
def train_model(model, n_epochs=100, lr=0.003, batch_size=2048, status_every=1, viz_every=1, warp_fn=None):
optimizer = optim.Adam(model.parameters(), lr=lr)
loss_fn = nn.MSELoss()
step, n_steps = 0, 100
device = next(model.parameters()).device
for epoch in range(n_epochs):
model.train()
pbar = tqdm(range(n_steps), leave=False)
for _ in pbar:
step += 1
optimizer.zero_grad()
# by randomly generating new data each step, we prevent the model from merely memorizing
source_samples = create_source_data(batch_size).to(device)
target_samples = create_target_data(batch_size).to(device)
t = torch.rand(source_samples.size(0), 1).to(device) # random times for traning
if warp_fn: t = warp_fn(t) # time warp is good for coverage but not as helpful for training as it is during integration/sampling
interpolated_samples = source_samples * (1 - t) + target_samples * t
line_directions = target_samples - source_samples
drift = model(interpolated_samples, t)
loss = loss_fn(drift, line_directions)
loss.backward()
optimizer.step()
status_str = f'Epoch [{epoch + 1}/{n_epochs}], Loss: {loss.item():.4f}'
pbar.set_description(status_str)
if (epoch + 1) % viz_every == 0:
model.eval()
clear_output(wait=True) # Clear previous plots
viz(val_points, target_samples[:val_points.shape[0]], model)
plt.show()
plt.close() # Close the figure to free memory
model.train()
if epoch==n_epochs-1: print(status_str) # keep last status from being cleared
return model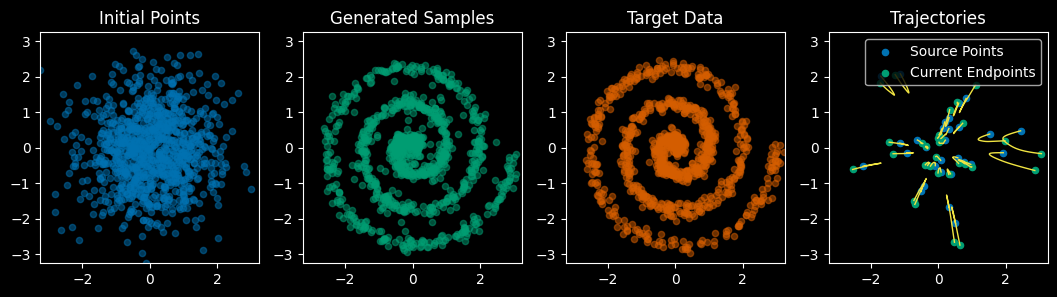
Epoch [100/100], Loss: 1.8315
Here’s an animation of integrating points along our model’s flow from start to finish:
Show code: animating points in flow
#| code-fold: true
#| code-summary: "Code for animating points in flow"
import matplotlib.animation as animation
from IPython.display import HTML, display, clear_output
from matplotlib import rc
import os
@torch.no_grad()
def create_flow_animation(start_dist, models, titles=None, figsize=None, n_frames=50,
step_fn=fwd_euler_step, n_steps=100, warp_fn=None, save_file=None, height=4):
"""
Create an animation showing multiple distribution flows
Args:
start_dist: Starting distribution
models: List of models to animate
titles: List of titles for each subplot (optional)
figsize: Figure size (optional)
n_frames: Number of animation frames
integrator: Integration function to use
jitter: Amount of jitter to add
save_file: Path to save animation (optional)
height: Height of each subplot
"""
plt.close('all') # Close all open figures
if not isinstance(models, list): models = [models]
n_plots = len(models)
if titles is None:
titles = [f'Flow {i+1}' for i in range(n_plots)]
elif len(titles) != n_plots:
raise ValueError(f"Number of titles ({len(titles)}) must match number of models ({n_plots})")
# Calculate figure size
if figsize is None:
figsize = [height * n_plots, height]
# Create subplots
fig, axes = plt.subplots(1, n_plots, figsize=figsize)
if n_plots == 1:
axes = [axes]
plt.close() # Close the figure immediately
# Initialize scatters and trajectories
scatters = []
all_trajectories = []
# Generate trajectories for each model
max_range = abs(start_dist).max().item()
for i, model in enumerate(models):
device = next(model.parameters()).device
end_dist, trajectories = integrate_path(model, start_dist.clone().to(device), n_steps=n_frames,
step_fn=step_fn, warp_fn=warp_fn, save_trajectories=True)
all_trajectories.append(trajectories.cpu())
scatters.append(axes[i].scatter([], [], alpha=0.6, s=10, color=wong_pink))
# Update max range
max_range = max(max_range, abs(end_dist.cpu()).max().item())
# Set up axes
for i, ax in enumerate(axes):
ax.set_xlim((-max_range, max_range))
ax.set_ylim((-max_range, max_range))
ax.set_aspect('equal')
ax.set_xticks([])
for spine in ['top', 'right', 'bottom', 'left']:
ax.spines[spine].set_visible(False)
ax.set_title(titles[i])
def init():
"""Initialize animation"""
for scatter in scatters:
scatter.set_offsets(np.c_[[], []])
return tuple(scatters)
def animate(frame):
"""Update animation frame"""
# Update axis limits (in case they need to be adjusted)
for ax in axes:
ax.set_xlim((-max_range, max_range))
ax.set_ylim((-max_range, max_range))
# Update scatter positions
for scatter, trajectories in zip(scatters, all_trajectories):
scatter.set_offsets(trajectories[frame].numpy())
return tuple(scatters)
# Create animation
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=n_frames, interval=20, blit=True)
# Handle saving or displaying
if save_file:
os.makedirs(os.path.dirname(save_file), exist_ok=True)
anim.save(save_file, writer='ffmpeg', fps=30)
return HTML(f"""<center><video height="350" controls loop><source src="{anim_file}" type="video/mp4">
Your browser does not support the video tag. </video></center>""")
else: # direct matplotlib anim offers better controls but makes ipynb file size huge
rc('animation', html='jshtml')
return HTML(anim.to_jshtml())
plt.close()
anim_file = 'images/particles_fm.mp4'
create_flow_animation(val_points.clone(), models=[fm_model], titles=['Flow Matching'],
n_frames=50, save_file=anim_file)So, even though we trained using trajectories that crossed, the model learned smooth and non-crossing (but curvy!) trajectories. Here’s a static plot of these:
Show code: make the static plot
@torch.no_grad()
def plot_training_trajectories_vs_learned_flow(model):
"""Compare training trajectories with learned flow field"""
plt.figure(figsize=(15, 5))
# 1. Plot some training trajectories
plt.subplot(131)
n_trajs = 50 # Number of trajectories to show
device = next(model.parameters()).device
source = create_gaussian_data(n_trajs)
target = create_square_data(n_trajs)
current_points = source.clone().to(device)
# Plot straight-line trajectories from source to target
times = torch.linspace(0, 1, 20)
for i in range(n_trajs):
traj = source[i:i+1] * (1 - times.reshape(-1, 1)) + target[i:i+1] * times.reshape(-1, 1)
plt.plot(traj[:, 0], traj[:, 1], 'b-', alpha=0.6, linewidth=3)
plt.title('Training Trajectories\n(with crossings)')
plt.axis('equal')
# 2. Plot learned flow field
plt.subplot(132)
x = torch.linspace(-3, 3, 20)
y = torch.linspace(-3, 3, 20)
X, Y = torch.meshgrid(x, y, indexing='ij')
points = torch.stack([X.flatten(), Y.flatten()], dim=1).to(device)
# with torch.no_grad():
# t = 0.5 # Show flow field at t=0.5
# ones = torch.ones(points.size(0), 1)
ones = torch.ones(points.size(0), 1).to(device)
t = ones * (0.5)
velocities = model(points, t).cpu()
#print("points.shape, ones.shape = ",points.shape, ones.shape)
#velocities = model(points, t*ones)
points = points.cpu()
plt.quiver(points[:, 0], points[:, 1],
velocities[:, 0], velocities[:, 1],
alpha=0.5, color=line_color, linewidth=3)
plt.title('Learned Flow Field\nat t=0.5')
plt.axis('equal')
# 3. Plot actual paths taken using learned flow
plt.subplot(133)
source = create_gaussian_data(n_trajs)
# Use RK4 to follow the learned flow
paths = []
n_steps = 20
dt = 1.0 / n_steps
with torch.no_grad():
ones = torch.ones(current_points.size(0), 1).to(device)
for i in range(n_steps):
paths.append(current_points.clone())
# RK4 step
t = ones * (i * dt)
k1 = model(current_points, t)
k2 = model(current_points + k1 * dt/2, t + dt/2)
k3 = model(current_points + k2 * dt/2, t + dt/2)
k4 = model(current_points + k3 * dt, t + dt)
current_points = current_points + (k1 + 2*k2 + 2*k3 + k4) * dt/6
paths = torch.stack(paths).cpu()
# Plot the actual paths
for i in range(n_trajs):
traj = paths[:, i, :]
plt.plot(traj[:, 0], traj[:, 1], color=line_color, alpha=0.5, linewidth=3)
plt.title('Actual Paths\nFollowing Learned Flow')
plt.axis('equal')
plt.tight_layout()
plt.savefig('images/cross_uncross_plot.png')
plt.show()
plt.close()
# Run the visualization
plot_training_trajectories_vs_learned_flow(fm_model)
Even though the trajectories on the right are smooth and non-crossing, their curviness means that we need to integrate slowly and carefully to avoid accruing significant error. Good news: the “Rectified Flow” paper of Liu et al
“Reflow” to Go Straighter & Faster
The Reflow idea is that, instead of randomly pairing source and target points when choosing straight trajectories, we use “simulated target points” by integrating the source points forward using the learned flow model. Then we use those endpoints as the targets and assume linear motion as before.

This has the effect of straightening out the curved trajectory of the flow matching model, making the new “reflowed” trajectories much easier and faster to integrate!
Essentially, Reflow is a “teacher-student” paradigm in which the (pre-)trained flow-matching model is the teacher, and the new Reflowed model is the student. One can also think of this as a kind of distillation, akin to “consistency models”
Before we can rely on those integrated endpoints, we should make a couple of improvements to how we use the model we just trained.
Upgrading Our Gear First
Neither of these upgrades require retraining the velocity model. They just help to make more efficient, accurate use of it while integrating (i.e., while moving data points along the flow) so we’ll have an effective “teacher” for the “student” Reflow model we’ll train below.
More Points Where Needed (via Time Warping)
You may notice that many of the trajectories are sharply curved in the middle but are straight near the start and end. Just as you’d slow down when driving around a sharp turn, we should take smaller integration steps in these curved regions for the sake of accuracy.
The idea of non-uniform temporal sampling appears throughout generative models. Esser et al.’s “FLUX” paper
- during training, we want good “coverage” to expose the model to significant places and times where it needs to learn to approximate the correct velocities, and
- during inference (i.e., integration), high-curvature segments will require shorter time steps to maintain accuracy (i.e., to keep from missing the intended destination).
One handy S-shaped time-warping function is this polynomial that lets us vary the concentration of points
Interactive Desmos Graph Link
The parameter $s$ is the slope at t=1/2, and controls where points concentrate: values between 0 and 1 give us more points in the middle, which is exactly what we want for these curved trajectories. The value $s=0.5$ is a good choice, as we’ll see shortly.
This approach can improve accuracy and/or require fewer total integration steps. Let’s look at the results of different amounts of time-warping around a simple parabola:
Show code: warp_time() and parabola example
def warp_time(t, dt=None, s=.5):
"""Parametric Time Warping: s = slope in the middle.
s=1 is linear time, s < 1 goes slower near the middle, s>1 goes slower near the ends
s = 1.5 gets very close to the "cosine schedule", i.e. (1-cos(pi*t))/2, i.e. sin^2(pi/2*x)"""
if s<0 or s>1.5: raise ValueError(f"s={s} is out of bounds.")
tw = 4*(1-s)*t**3 + 6*(s-1)*t**2 + (3-2*s)*t
if dt: # warped time-step requested; use derivative
return tw, dt * 12*(1-s)*t**2 + 12*(s-1)*t + (3-2*s)
return tw
from functools import partial
parab = lambda x: 4*(x-0.5)**2 # curve shape
d_parab = lambda x: 8*(x-0.5) # derivative
ds = lambda x: torch.sqrt(1 + d_parab(x)**2) # differential arc length
def calculate_total_arc_length(n=1000):
"""Calculate the total arc length of the parabola y = 4(x - 0.5)**2 from x=0 to x=1"""
x_values = torch.linspace(0, 1, n)
arc_length_values = ds(x_values)
total_arc_length = torch.trapz(arc_length_values, x_values)
return total_arc_length
def fake_velocity_model(loc, t, speed=1.0):
"""For demo purposes only: Follow a parabolic path and move at unit speed
Compute the x and y components of the velocity along the parabola y = 4(x - 0.5)^2"""
x, y = loc[:, 0], loc[:, 1]
slope = d_parab(x)
direction = torch.stack([torch.ones_like(slope), slope], dim=1)
magnitude = torch.norm(direction, dim=1, keepdim=True)
unit_velocity = direction / magnitude
return unit_velocity*speed
@torch.no_grad()
def integrate_motion_along_parabola(
model, initial_points, n_steps=30, step_fn=fwd_euler_step, s=0.5,):
"""one-off integrator used only for this one visualization figure. don't use for anything else"""
current_points = initial_points.clone()
trajectories = [current_points.cpu().clone()]
ts = torch.linspace(0,1.0, n_steps)
ts = warp_time(ts, s=s) # here's the time worpage
speed = calculate_total_arc_length() # Total travel time is 1.0 so speed "=" distance
scaled_model = partial(model, speed=speed)
with torch.no_grad():
for i in range(n_steps-1):
current_points = step_fn( scaled_model , current_points.clone(), ts[i], ts[i+1]-ts[i])
trajectories.append(current_points.cpu().clone())
return torch.stack(trajectories)
@torch.no_grad()
def viz_parabola_with_steps(step_fn=fwd_euler_step, n_steps=28):
"""varies warp parameter s and integrates along a parabola"""
plt.close()
t_curve = torch.linspace(0,1,100)
n_t_points = n_steps # 28 if step_fn==fwd_euler_step else 6
t_points = torch.linspace(0,1,n_t_points)
n_s = 6 # number of different s values to show
fig, ax = plt.subplots(1, n_s, figsize=(n_s*2.8, 3))
plt.suptitle(f"Integration scheme = {step_fn.__name__}", fontsize=16, y=1.05)
initial_points = torch.tensor([[0,1]]) # one point in the top left
for i, s in enumerate(torch.linspace(.25, 1.5, n_s)): # warp time by different amounts via s parameter
ax[i].plot(t_curve, parab(t_curve)) # solid line showing path
traj = integrate_motion_along_parabola(fake_velocity_model, initial_points, n_steps=n_t_points,
s=s, step_fn=step_fn).squeeze()
err_str = f"\nerror={F.mse_loss(parab(traj[:,0]),traj[:,1]):.3g}"
ax[i].scatter(traj[:,0], traj[:,1], label=f's = {s:.2f}{err_str}', color=(wong_cmap*2)[i])
legend = ax[i].legend(loc='upper center', frameon=False, markerscale=0, handlelength=0, fontsize=12)
for text in legend.get_texts():
text.set_ha('center')
if abs(s-1.0) < 1e-3: ax[i].set_title('Even Spacing')
ax[0].set_title('More Points in Middle')
ax[-1].set_title('More Points at Ends')
plt.show()
plt.close()
viz_parabola_with_steps() 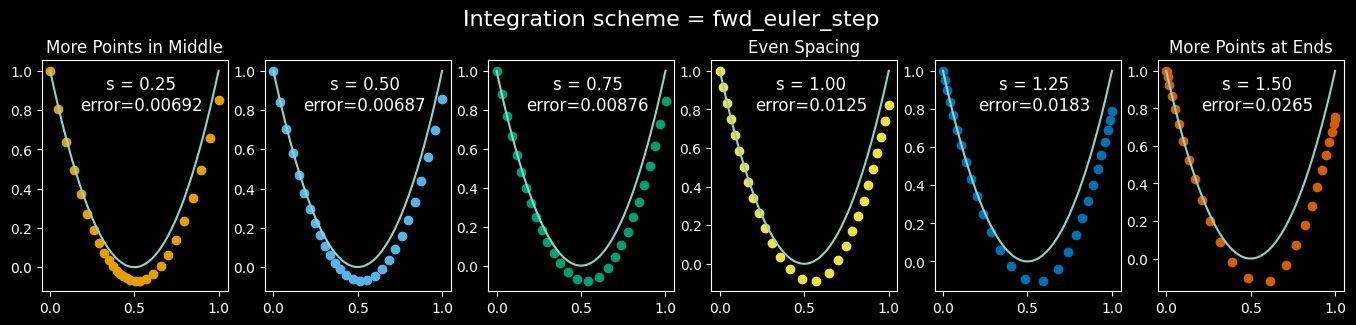
While the results for $s=0.5$ are better than the others, we see that none of these examples make it all the way around the parabola (to the point (1,1))! If we’re going to be using the endpoints integrated from the flow matching model as proxies for the true target data, we should have some confidence that those endpoints are actually “reaching” the target data. We could add more (smaller) steps to the integration, but there’s another way: upgrade the integration (i.e. sampling) operation to a higher order of accuracy.
Better Integration / Sampling
Although forward Euler is surprisingly popular in ML circles, those with simulation backgrounds eye it with suspicion: despite being fast (per step) and easy to implement, it’s also highly inaccurate and can lead to instabilities. The poor accuracy may not be an issue when everything’s an approximation anyway, but we can do a lot better.
People who work with diffusion models know this. For example, Katherine Crowson’s k-diffusion package
Show code: RK4 step
def rk4_step(f, # function that takes (y,t) and returns dy/dt, i.e. velocity
y, # current location
t, # current t value
dt, # requested time step size
):
k1 = f(y, t)
k2 = f(y + dt*k1/2, t + dt/2)
k3 = f(y + dt*k2/2, t + dt/2)
k4 = f(y + dt*k3, t + dt)
return y + (dt/6)*(k1 + 2*k2 + 2*k3 + k4)
viz_parabola_with_steps(step_fn=rk4_step, n_steps=6) 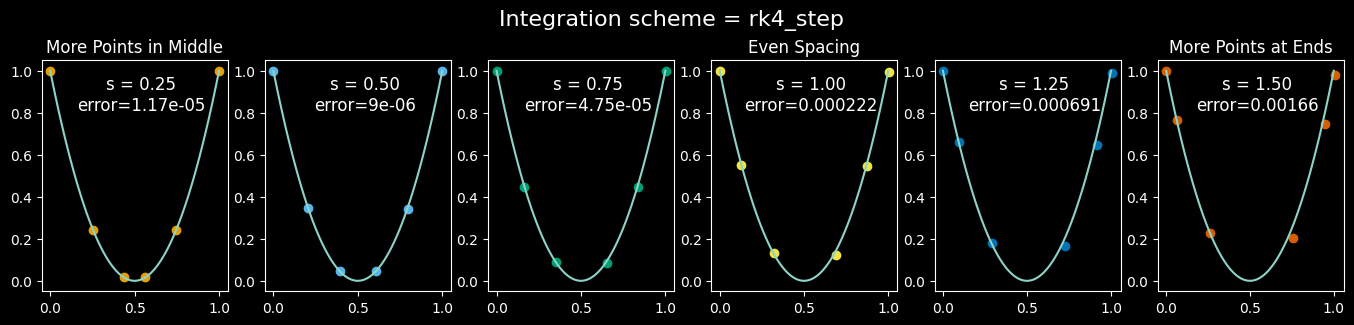
It’s cool how the RK4 results, despite showing much less error than the Euler results, actually involve less computational cost in terms of total number of function evaluations, although the RK4 scheme needs 4 times the storage compared to forward Euler. (The good news is that no PyTorch gradients need to be stored; the integrator is only ever used when the model is in “eval” mode.)
Learning to “Reflow”
When we train the “Reflowed” model, aka the student model, note that the “target data” will no longer be supplied by the true target data anymore. Rather, we will be using the trajectory endpoints integrated/generated using the teacher model, i.e. the pretrained flow matching model.
So we might ask, “How close of an approximation are those learned flow endpoints to the real thing?” We’re going to be approximating an approximation, but how good is the first approximation?
Let’s take a brief look…
Show code
#| code-fold: true
#| code-summary: "quick check of how our flow endpoints are looking"
pretrained_model = fm_model
pretrained_model.eval()
reflow_targets = integrate_path(pretrained_model, val_points.to(device), n_steps=8, step_fn=rk4_step, warp_fn=warp_time).cpu()
fig, ax = plt.subplots(1,3, figsize=(10,3))
for i, [data, color, label] in enumerate(zip([val_points, reflow_targets, target_samples],
[source_color, pred_color, target_color],
['Source Data', 'Learned Flow Endpoints', 'True Target Data'])):
ax[i].scatter(data[:,0], data[:,1], color=color, label=label, alpha=0.6)
ax[i].set_aspect('equal')
ax[i].set_title(label)
plt.show()
plt.close()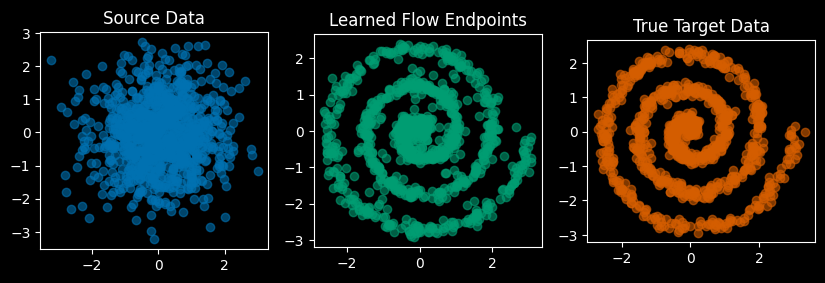
….ok, so we see the learned outputs are a bit different from the true data, but they’re not bad. Let’s now train the “reflow” model.
Train the Reflowed Model
There’s one small but crucial change from the previous training code to this one, namely what we use as target data:
## target_samples = create_target_data(batch_size) # Previous "random pairing"
target_samples = integrator(pretrained_model, source_samples) # Reflow!
Show code: new training loop w/ ReFlowed targets
def train_reflow_model(model, pretrained_model=None,
n_epochs=40, lr=0.001, batch_size=2048,
status_every=1, viz_every=1, # in epochs
new_points_every=1, # in steps
warp_fn=warp_time,
step_fn=rk4_step, # rk4 so we get high-quality outputs while reflowing
):
"""This is almost IDENTICAL to the previous training routine.
The difference is the change in "target_samples" via what the RF authors call "ReFlow":
Instead of (randomly) paring source points with points in the "true target distribution",
we use the pretrained/teacher model to integrate the source points to their (predicted) flow endpoints
and use THOSE as the "target" values.
"""
optimizer = optim.Adam(model.parameters(), lr=lr)
loss_fn = nn.MSELoss()
step, n_steps = 0, 100
device = next(model.parameters()).device
for epoch in range(n_epochs):
model.train()
pbar = tqdm(range(n_steps), leave=False)
for _ in pbar:
step += 1
optimizer.zero_grad()
if step % new_points_every == 0: # you could in theory not draw new points with each step, though we will.
source_samples = create_source_data(batch_size).to(device)
if pretrained_model: # HERE is the ReFlow operation...
target_samples = integrate_path(pretrained_model, source_samples, step_fn=rk4_step, warp_fn=warp_time, n_steps=20)
else:
target_samples = create_target_data(batch_size) # this function also supports fm models from scratch
t = torch.rand(source_samples.size(0), 1).to(device) # random times for training
if warp_fn: t = warp_fn(t) # time warp here (different from use in integrator!) helps focus "coverage" i.e. sampling the space
interpolated_samples = source_samples * (1 - t) + target_samples * t
v = model(interpolated_samples, t)
line_directions = target_samples - source_samples
loss = loss_fn(v, line_directions)
loss.backward()
optimizer.step()
pbar.set_description(f'Epoch [{epoch + 1}/{n_epochs}], Loss: {loss.item():.4g}')
if (epoch + 1) % viz_every == 0:
model.eval()
clear_output(wait=True) # Clear previous plots
viz(val_points, target_samples[:val_points.shape[0]], model) # don't need rk4 for reflow'd model viz b/c paths r straight
plt.show()
plt.close() # Close the figure to free memory
model.train()
return modelimport copy
# Note that the student/reflow model could have a simpler architecture
# than the teacher/pretrained model, but... we'll just keep 'em the same :shrug:
reflowed_model = copy.deepcopy(pretrained_model) # no need to start from scratch, use teacher's weights
reflowed_model.train() # make sure we have gradients turned on
reflowed_model = train_reflow_model(reflowed_model, pretrained_model=pretrained_model)
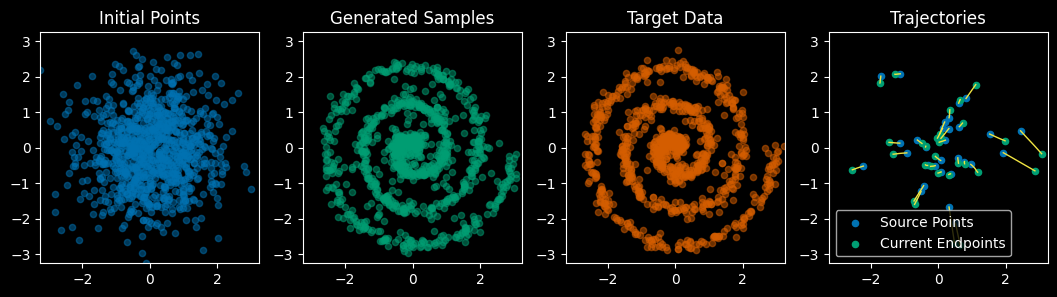
Now look how straight the trajectories are! Let’s compare animations of the original flow matching model with the “Reflowed” model:
#| code-fold: true
#| code-summary: "Making movie for particle animation comparison"
rect_eval = reflowed_model.eval()
anim_file = "images/particles_fm_vs_rf.mp4"
create_flow_animation(val_points.clone(), models=[pretrained_model, reflowed_model],
n_frames=50, titles=['Flow Matching','Reflowed Flow'], save_file=anim_file)
Notice how the flow matching trajectories on the left have the data moving inward a ways and then back out, whereas the reflowed trajectories move directly from start to finish with no backtracking.
The next movie shows an animation of “streamlines” with arrows for the local vector field. Note how the shapes on the right change very little over time compared to those on the left. We’ll say a bit more about that below.
Show code: streamline animation
@torch.no_grad()
def create_streamline_animation(start_dist, model, model2=None, n_frames=50, show_points=False, titles=None,
step_fn=fwd_euler_step, # euler's ok for reflowed model bc/paths are straight
save_file=None,
):
"""Create an animation showing distribution flow with streamplot background"""
device = next(model.parameters()).device
figsize = [5,5]
if titles is None:
titles = ['Flow Matching']
if model2: titles += ['Reflowed Model']
if model2:
figsize[0] *= 2
n_plots = 1 + (model2 is not None)
fig, ax = plt.subplots(1, n_plots, figsize=figsize)
if n_plots==1: ax = [ax]
plt.close()
end_dist, trajectories = integrate_path(model, start_dist.clone().to(device), n_steps=n_frames, step_fn=step_fn, warp_fn=warp_time, save_trajectories=True)
scatter = ax[0].scatter([], [], alpha=0.6, s=10, color=wong_pink, zorder=1)
if model2:
_, trajectories2 = integrate_path(model2, start_dist.clone().to(device), n_steps=n_frames, step_fn=step_fn, warp_fn=warp_time, save_trajectories=True)
scatter2 = ax[1].scatter([], [], alpha=0.6, s=10, color=wong_pink, zorder=1)
max_range = max( abs(start_dist).max().item(), abs(end_dist).max().item() )
for i in range(len(ax)):
ax[i].set_xlim((-max_range, max_range))
ax[i].set_ylim((-max_range, max_range))
ax[i].set_aspect('equal')
if titles: ax[i].set_title(titles[i])
# Create grid for streamplot
grid_dim = 50
x = np.linspace(-max_range, max_range, grid_dim)
y = np.linspace(-max_range, max_range, grid_dim)
X, Y = np.meshgrid(x, y)
# Convert grid to torch tensor for model input
grid_points = torch.tensor(np.stack([X.flatten(), Y.flatten()], axis=1), dtype=torch.float32).to(device)
color = wong_pink if show_points else (0,0,0,0)
dt = 1.0 / n_frames
def init():
for i in range(len(ax)):
ax[i].clear()
ax[i].set_xlim((-max_range, max_range))
ax[i].set_ylim((-max_range, max_range))
scatter.set_offsets(np.c_[[], []])
if model2:
scatter.set_offsets(np.c_[[], []])
return (scatter,scatter2)
return (scatter,)
def animate(frame):
for i in range(len(ax)):
ax[i].clear()
ax[i].set_xlim((-max_range, max_range))
ax[i].set_ylim((-max_range, max_range))
if titles: ax[i].set_title(titles[i])
ax[i].set_xticks([])
ax[i].set_yticks([])
for spine in ['top','right','bottom','left']:
ax[i].spines[spine].set_visible(False)
# Update scatter plot
current = trajectories[frame]
scatter = ax[0].scatter(current[:, 0], current[:, 1], alpha=0.6, s=10, color=color, zorder=1)
if model2:
current2 = trajectories2[frame]
scatter2 = ax[i].scatter(current2[:, 0], current2[:, 1], alpha=0.6, s=10, color=color, zorder=1)
# Calculate vector field for current time
t = torch.ones(grid_points.size(0), 1) * (frame * dt)
t = warp_time(t).to(device)
velocities = model(grid_points, t).cpu()
U = velocities[:, 0].reshape(X.shape)
V = velocities[:, 1].reshape(X.shape)
x_points = np.linspace(-max_range, max_range, 15)
y_points = np.linspace(-max_range, max_range, 15)
X_arrows, Y_arrows = np.meshgrid(x_points, y_points)
start_points = np.column_stack((X_arrows.ravel(), Y_arrows.ravel()))
ax[0].streamplot(X, Y, U.numpy(), V.numpy(),
density=5, # Controls line spacing
color=line_color, # (0, 0, 1, 0.7),
linewidth=0.8, maxlength=0.12,
start_points=start_points, # This should give more arrows along paths
arrowsize=1.2,
arrowstyle='->')
if model2:
velocities2 = model2(grid_points, t).cpu()
U2 = velocities2[:, 0].reshape(X.shape)
V2 = velocities2[:, 1].reshape(X.shape)
start_points2 = np.column_stack((X_arrows.ravel(), Y_arrows.ravel()))
ax[1].streamplot(X, Y, U2.numpy(), V2.numpy(),
density=5, # Controls line spacing
color=line_color, # (0, 0, 1, 0.7),
linewidth=0.8, maxlength=0.12,
start_points=start_points2, # This should give more arrows along paths
arrowsize=1.2,
arrowstyle='->')
# Update particle positions
t = torch.ones(current.size(0), 1) * (frame * dt)
t, dtw = warp_time(t, dt=dt)
velocity = model(current.to(device), t.to(device)).cpu()
current = current + velocity * dtw
if model2:
velocity2 = model2(current2.to(device), t.to(device)).cpu()
current2 = current2 + velocity2 * dtw
return (scatter, scatter2,)
return (scatter,)
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=n_frames, interval=20, blit=False)
if save_file:
anim.save(save_file, writer='ffmpeg', fps=30)
return HTML(f"""<center><video height="350" controls loop><source src="{save_file}" type="video/mp4">
Your browser does not support the video tag.</video></center>""")
else:
rc('animation', html='jshtml')
return HTML(anim.to_jshtml())
save_file = 'images/fm_vs_rf_streamvecs.mp4'
create_streamline_animation(val_points, fm_model, model2=reflowed_model, n_frames=50, save_file=save_file)#, show_points=True)Connecting with Other Models
From Dots to Images, Audio, etc..
How to move on from 2D dots to things like images, text, audio,…etc? We need only consider that the dimensionality of the velocity model is the same as that of the data itself. Put differently, one can regard the velocity model as supplying a tiny “change” to the data, whatever form that data is in. And the “straight line” trajectory used during training? That’s just linear interpolation between the (initially randomly-paired) source data and the target data. So for images, we will get a “velocity image”, which will tell us how to change the R,G,B values of every pixel in an image. This is where U-Nets and Attention come into play, to efficiently compute the “image-to-image” task of supplying a “velocity image” given an input image distribution (which may just be noise). For audio, regardless of the representation, the velocity model will tell us how to slightly change the component values in that representation. We then just integrate all the little changes as we did with the dots.
- The reader may wish to view an MNIST image example such as Tadao Yamaoka’s
.
Diffusion Models
Diffusion models, aka “score-based models,” share similarities with flow models in that both learn vector fields that transform points in the sample space. In “standard” diffusion models (DDPMs,
Optimal Transport
Interesting observation: See how the Reflowed streamlines in the last movie are approximately stationary (i.e., time-independent)? This connects nicely with Optimal Transport theory, where the Benamou-Brenier formulation
Normalizing Flows
Normalizing flows have the property that they preserve overall probability throughout the flow process. While this would seem to be a nice constraint to satisfy, it appears to be unnecessary for “getting the job done” yet it may even limit the expressiveness of the model compared to the kinds of flows we’ve been talking about in this post. Note: Since I’m pushing a “physics perspective,” a similar “conservation” property arises in the phase space flows of Hamiltonian mechanics, namely that they preserve areas and volumes via Liousville’s Theorem
Summary
We’ve seen that flow matching and rectified flow models can be conceptualized and developed using simple ideas from basic physics. This simplicity, coupled with their power and flexibility, has fueled their rise to state-of-the-art performance. While the toy problem presented here is less demanding than applications like high-resolution image synthesis (for which readers should consult relevant literature