Parameter-Efficient and Stable Singular Value Adaptation for Pre-Trained Models

We observe that the Q, K, O, and V matrices in attention layers can inherently be absorbed and decomposed into four head-wise orthogonal matrices and two sets of singular values without any loss. After orthogonalization, we freeze the singular vectors and fine-tune only the singular values, enabling stable fine-tuning constrained to the original latent space, which achieves a 5.4% improvement over LoRA across eight commonsense reasoning datasets. Additionally, this absorb-decompose operation eliminates redundant vectors losslessly and reduces the encoder parameters of Whisper-large-v3 by 46.42% without requiring additional training.

Introduction

Fine-tuning large language models (LLMs) is highly effective for enhancing downstream task performance. However, fine-tuning very large models is costly. For instance, 16-bit fine-tuning of GPT-3 175B consumes 1.2 TB of VRAM , while LLaMA 65B model requires over 780 GB of GPU memory . To address this, parameter-efficient fine-tuning (PEFT) methods, such as Low-Rank Adaptation (LoRA) , have been developed to reduce memory usage and parameter requirements while maintaining performance without adding inference latency.

Shuttleworth et al. recently analyzed how fine-tuning alter pre-trained models by examining the spectral properties of weight matrices. They found that LoRA introduces high-ranking singular vectors, termed ‘intruder dimensions’, which are absent in full fine-tuning. Models fine-tuned with LoRA tend to forget more of the pre-training distribution and show less robust continual learning compared to full fine-tuning.

PiSSA and SVFT applies SVD to the pre-trained matrix. SVFT freezing the singular vectors and fine-tuning only the singular values. By avoiding the introduction of ‘intruder dimensions,’ this approach helps stabilize the training process. However, although it reduces the number of trainable parameters, decomposing a matrix $W \in \mathbb{R}^{m \times n}$ into orthogonal matrices $U \in \mathbb{R}^{m \times \text{min}(m,n)}$, and $V \in \mathbb{R}^{\text{min}(m,n) \times n}$, and diagonal matrix $S \in \mathbb{R}^{\text{min}(m,n)\times\text{min}(m,n)}$, introduces significant additional parameters and computational overhead. When m = n , this overhead exceeds $3\times$ the original cost. PiSSA slicing the principal singular values and singular vectors for fine-tuning while keeping the remaining components frozen. This avoids the twofold computational cost but limits adjustments to only part of the orthogonal bases.

A key question then arises: how can we efficiently fine-tune within the latent space of pre-trained models?

In this work, we observe that each attention layer naturally contains two pairs of matrices, $W_Q$ and $W_K^T$, as well as $W_V$ and $W_O$, which can be absorbed into head-wise low-rank matrices $W_{QK}\in\mathbb{R}^{h\times D\times D}$ and $W_{VO}\in\mathbb{R}^{h\times D\times D}$, where the ranks satisfy $r_{qk} \leq d$ and $ r_{vo} \leq d$. By decomposing $W_{QK}$ and $W_{VO}$ with SVD and removing singular vectors corresponding to zero singular values, we obtain orthogonal bases without increasing and even reducing the number of frozen parameters. These frozen bases maintain stability during fine-tuning, while the corresponding singular values, with minimal parameter overhead, enable efficient fine-tuning.

Summary of Contributions:

Orthogonalization via Absorb-Decompose: We discovered that the $W_Q$, $W_K$ and $W_V$,$W_O$ matrices in attention mechanisms can be orthonormalized through a Absorb-Decompose method. This transformation preserves the model’s original capabilities.
Reducing Redundant Parameters: Orthogonalizing attention heads effectively eliminates redundant parameters. Applying Absorb-Decompose to the encoder of Whisper-large-v3 reduces 56.01% of the parameters in $W_Q$ and $W_K$, and 36.82% in $W_V$ and $W_O$, without any loss of performance, even without additional training.
Efficient and Stable Fine-Tuning: By freezing the orthogonal bases and fine-tuning only their linear combinations, we introduce Parameter-Efficient and Stable Singular value Adaptation (PESSA). Applying PESSA to fine-tune LLaMA-2-7B achieves an average improvement of 5.4% over LoRA and 4.4% over DoRA across 8 commonsense reasoning fine-tuning tasks.

LoRA integrates trainable adapters into linear layers, allowing these adaptations to be re-parameterized back into the standard model structure after fine-tuning. This approach has gained widespread adoption for its ability to preserve the model’s original architecture while enabling efficient fine-tuning. Building on LoRA, AdaLoRA dynamically learns the rank size required for LoRA in each model layer, optimizing parameter efficiency. DeltaLoRA enhances LoRA’s representational capacity by directly updating the original weights of the model using parameters from adapter layers. LoSparse incorporates LoRA to mitigate the risk of pruning overly expressive neurons. DoRA introduces a magnitude component to learn the scale of $\Delta W$, while using the original AB as the direction component of $\Delta W$.

PiSSA focuses on the impact of initialization on gradient directions, firstly applying singular value decomposition (SVD) to the original matrix and fine-tuning the principal singular values and corresponding singular vectors. This initialization approach leads to faster convergence, improved performance, and reduced quantization error. Following PiSSA, LoRA-XS , LaMDA and SVFT , perform singular value decomposition on the original matrix, freezing the singular vectors while fine-tuning the singular values to reduces the trainable parameters. Among them, LoRA-XS and LaMDA fine-tune only a subset of singular values, while SVFT adjusts all singular values. OLoRA leverages orthonormal matrix initialization through QR decomposition. CorDA , MiLoRA , LoRA-GA , LoRA-Pro , and EVA utilize SVD in different ways to initialize adapters. CorDA and EVA decompose data for initialization, MiLoRA leverages the smaller singular values of matrices, while LoRA-GA and LoRA-Pro decompose the update directions from full fine-tuning. SVDQuant addresses outliers by shifting them from activations to weights and employs a high-precision low-rank branch to integrate the weight outliers using SVD.

Parameter-Efficient and Stable Singular value Adaptation

Figure 1. Workflow of Parameter-Efficient and Stable Singular Value Adaptation (PESSA). Frozen parameters are represented in blue, while trainable parameters are highlighted in orange. The left diagram illustrates a standard multi-head attention mechanism. In PESSA, we absorb $W_Q$, $W_K^T$ and $W_V$, $W_O$ into two low-rank matrices, $W_{QK}$ and $W_{VO}$, respectively. These matrices are then decomposed using SVD. The original attention head matrices are replaced by singular vectors associated with non-zero singular values, while the singular values are inserted between the vectors to enable fine-tuning. This transformation yields a module that is functionally equivalent to the original attention layer.

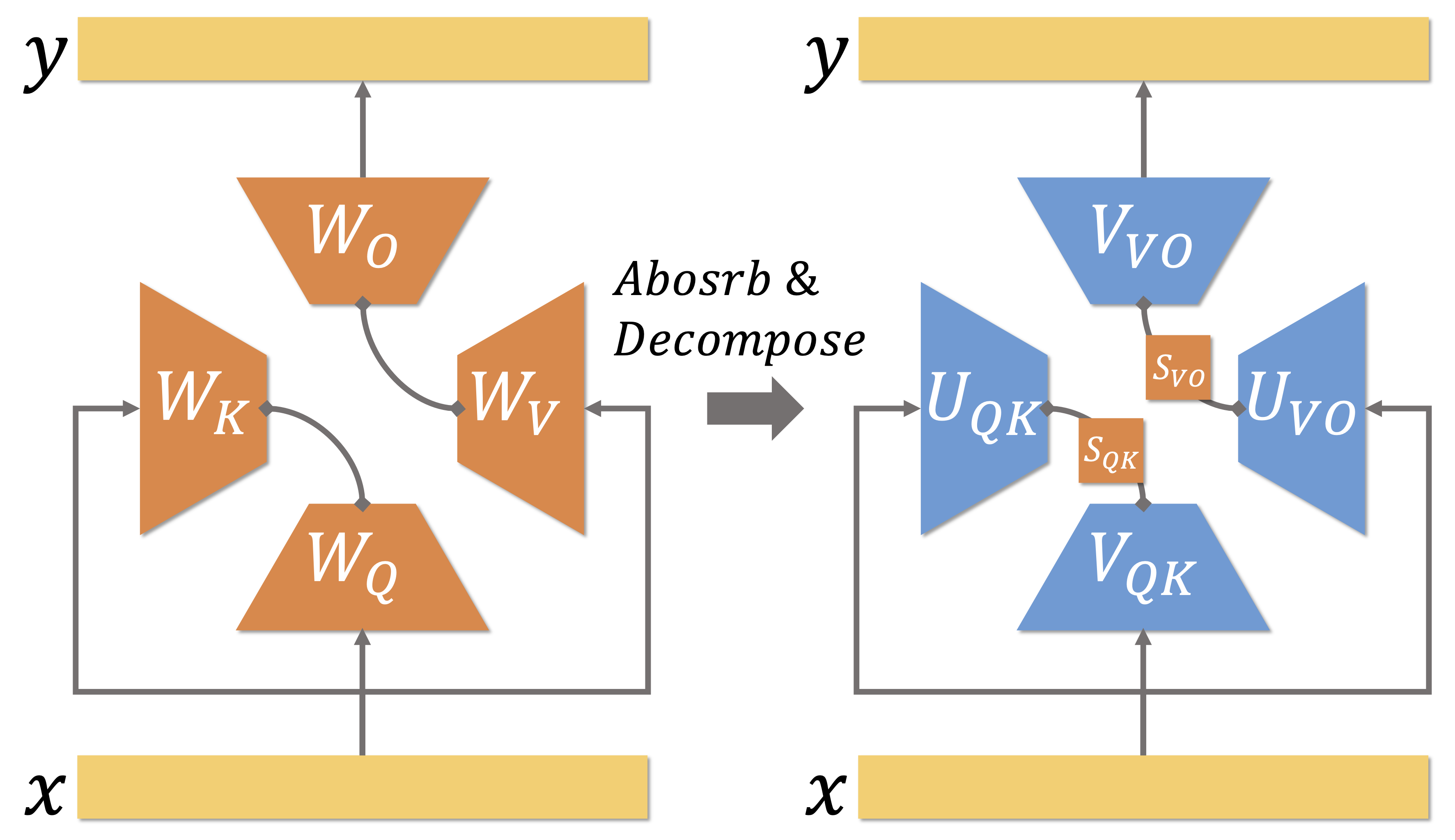
Absorb and Decompose

For Multi-Head Self-Attention, $X\in \mathbb{R}^{b\times n\times D}$, $W_Q\in \mathbb{R}^{D\times h\times d}$, $W_K\in \mathbb{R}^{D\times h\times d}$, $W_V\in \mathbb{R}^{D\times h\times d}$, $W_O\in \mathbb{R}^{h\times d\times D}$.

Where $b$, $n$ and $D$ represent the batch size, the seqence length and the dimension of $X$. $h$ and $d$ is the number of heads and the dimension of head for $W_Q$, $W_K$ and $W_V$, $W_O$.

The process of absorbing and decomposing $W_Q$ and $W_K$ can be represented as follows:

\[\text{attn(Q, K)}=\text{softmax}(\frac{QK^T}{\sqrt{d}}), \quad \text{$Q=XW_Q\in \mathbb{R}^{b\times h\times n\times d}$, $K=XW_K\in \mathbb{R}^{b\times h\times n\times d}.$}\] \[=\text{softmax}(\frac{XW_QW_K^TX^T}{\sqrt{d}}), \quad \text{$W_QW_K^{T}=W_{QK}\in \mathbb{R}^{h\times D\times D}.$}\] \[=\text{softmax}(\frac{XW_{QK}X^T}{\sqrt{d}}), \quad \text{$W_{QK}=USV=U_{[:,:,:r_{qk}]}S_{[:,:r_{qk},:r_{qk}]}V_{[:,:r_{qk},:]}=U_{QK}S_{QK}V_{QK}, r_{qk}\leq d.$}\] \[=\text{softmax}(\frac{XU_{QK}S_{QK}V_{QK}X^T}{\sqrt{d}}), \quad \text{$U_{QK}\in \mathbb{R}^{D\times h\times r_{qk}}$, $S_{QK}\in \mathbb{R}^{h\times r_{qk} \times r_{qk}}$, $V_{QK}\in \mathbb{R}^{h\times r_{qk} \times D}.$}\]

Through this series of transformations, $W_Q$ and $W_K$ can be equivalently replaced by orthogonal vectors $U_{QK}$ and $V_{QK}$, along with the diagonal matrix $S_{QK}$.

The process of absorbing and decomposing $W_V$ and $W_O$ can be represented as follows:

\[Y=\text{attn(Q, K)}VW_O, \quad \text{$V=XW_V\in \mathbb{R}^{b\times h\times n\times d}$},\] \[=\text{attn(Q, K)}XW_VW_O, \quad \text{$W_VW_O=W_{VO}\in \mathbb{R}^{h\times D\times D}$}\] \[=\text{attn(Q, K)}XW_{VO}, \quad \text{$W_{VO}=USV=U_{[:,:,:r_{vo}]}S_{[:,:r_{vo},:r_{vo}]}U_{[:,:r_{vo},:]}=U_{VO}S_{VO}V_{VO}, r_{vo}\leq d$.}\] \[=\text{attn(Q, K)}XU_{VO}S_{VO}V_{VO}, \quad \text{$U_{VO}\in \mathbb{R}^{D\times h\times r_{vo}}$, $S_{VO}\in \mathbb{R}^{h\times r_{vo} \times r_{vo}}$, $V_{VO}\in \mathbb{R}^{h\times r_{vo} \times D}.$}\]

Through this series of transformations, $W_V$ and $W_O$ can be equivalently replaced by orthogonal vectors $U_{VO}$ and $V_{VO}$, along with the diagonal matrix $S_{VO}$.

Parameter-Efficient and Stable Fine-Tuning

The proposed Absorb-Decompose operation effectively reduces linear dependencies in $W_Q$, $W_K$, $W_V$, and $W_O$. During the decomposition of $W_{QK}$ and $W_{VO}$, it generates vectors with dimensions smaller than the head dimension, enabling a training-free pruning process.

Unlike traditional pruning, which allows for lossy pruning followed by retraining to recover model accuracy, pruning large pre-trained models presents unique challenges. The pretraining of such models relies on vast, often inaccessible datasets. As a result, while retraining may achieve strong performance on certain benchmarks, it can fail on other tasks or even introduce safety risks. This makes training-free pruning particularly critical.

Thanks to the Absorb-Decompose method, which orthogonalizes the original $W_Q$-$W_K$ and $W_V$-$W_O$ pairs in attention layers, we obtain a moderate number of singular values. For comparison, SVFT decomposes the entire matrix and produces singular values $S \in \mathbb{R}^{\text{min}(m, n) \times \text{min}(m, n)}$. One approach treats $S$ as a vector, significantly reducing the number of trainable parameters but limiting expressive capacity since it can only scale singular vectors without learning their linear combinations. Another approach considers $S$ as a full matrix, which, for attention layers where $m = n$ , results in a parameter size equivalent to the original matrix, making it less practical. To balance these trade-offs, SVFT adopts a sparse representation of $ S $, fine-tuning only its diagonal elements, a small boundary width, and a fixed sparse pattern. While this improves efficiency, it is less flexible than a structured format.

Our proposed PESSA method strikes a balance between these extremes by learning head-wise singular values $S \in \mathbb{R}^{h \times d \times d}$, where $d$ is the attention head dimension. For instance, in LLaMA-2-7B, $h = 32$ and $d = 128$ , resulting in a parameter count comparable to a rank-$64$ LoRA configuration. PESSA allows orthogonal singular vectors within each head to freely combine, significantly enhancing expressive capacity.

By leveraging the benefits of Absorb and Decompose operations, $W_Q$, $W_K$, $W_V$, and $W_O$ can be equivalently represented using smaller, mutually orthogonal singular vectors and their corresponding singular values. For parameter-efficient and stable fine-tuning, the gradients of the orthogonal bases are frozen and used only in the forward pass, while only the singular values are fine-tuned, enabling updates within the latent space of the pre-trained model.

Due to the RoPE applied between $W_Q$ and $W_K$ in LLaMA-2-7B, the Absorb-Decompose operation cannot be directly applied. For such cases, we replace SVD with QR decomposition and decompose $W_Q$ and $W_K$ into orthogonal matrices and upper triangular matrices. We freeze the orthogonal matrices and fine-tune the upper triangular matrices. Combined with the singular value matrix obtained by performing Absorb-Decompose on $W_V$ and $W_O$, the total number of trainable parameters in this setup is equivalent to fine-tuning $W_Q$, $W_K$, and $W_V$ with rank-$64$ LoRA.

Using PESSA for fine-tuning requires reinitializing the model only at the start. After training, $S_{QK}$ and $S_{VO}$ can be merged back into $U_{QK}$ and $U_{VO}$, ensuring no additional inference overhead.

Experiment

Absorb-Decompose for Pruning

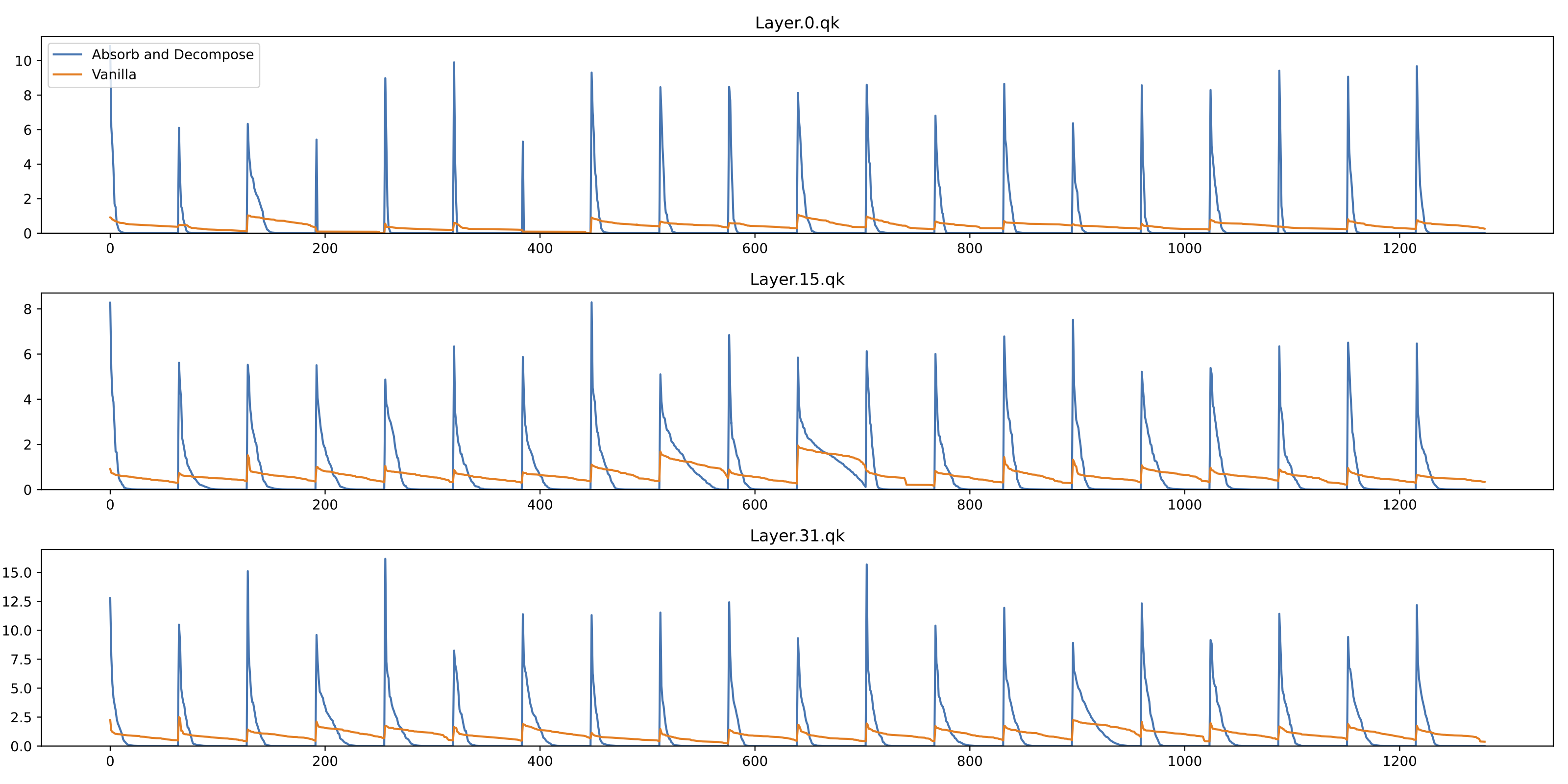
We selected the Whisper-large-v3 model , a Transformer-based encoder-decoder architecture with 1.55 billion parameters. It is trained simultaneously on multilingual speech recognition and speech translation tasks. We applied the Absorb-Decompose method across all 32 attention layers in the encoder. Figure 2 illustrates the singular values $S_{QK}$ obtained through this method. For comparison, we also computed the Euclidean norm for each dimension and ranked them in descending order within each attention head.

Figure 2: The $L_2$-norm for the 0-th, 15-th, and 31-st attention layers in the Whisper-large-v3 encoder. The blue line represents the results after redundancy removal using the Absorb-Decompose method, while the orange line depicts the $L_2$-norm directly computed for each dimension.

As shown in Figure 2, although the $L_2$-norms for dimensions in the 0-th and 15-th layers are small, their distribution across dimensions is relatively uniform, with less dimension reduced to zero. Removing such dimensions indiscriminately could significantly harm model performance. In contrast, the Absorb-Decompose method concentrates these parameters into a small subset of bases, resulting in many singular values being reduced to zero. This allows their corresponding singular vectors to be safely pruned.

We also observed that different layers exhibit varying degrees of low-rank properties. Early layers tend to have higher redundancy, while later layers contain more task-relevant independent vectors. To address this, we applied a unified, small threshold across all layers. Singular values below this threshold, along with their corresponding singular vectors, were pruned. Our findings demonstrate that the Absorb-Decompose method enables a high rate of training-free pruning, effectively reducing model complexity without compromising its performance.

Next, we present an example to intuitively demonstrate the effectiveness of this training-free pruning approach. We use a audio input from the librispeech_long dataset . The waveform of this input is visualized in Figure 3 for reference.

We first use Whisper-large-v3 directly to recognize the audio. The baseline recognition output is as follows:

Mr. Quilter is the apostle of the middle classes, and we are glad to welcome his gospel. 
Nor is Mr. Quilter's manner less interesting than his matter. 
He tells us that at this festive season of the year, with Christmas and roast beef looming before us, similes drawn from eating and its results occur most readily to the mind. 
He has grave doubts whether Sir Frederick Layton's work is really Greek after all, and can discover in it but little of rocky Ithaca. 
Linnell's pictures are a sort of Up Guards and Adam paintings, and Mason's exquisite idles are as national as a jingo poem. 
Mr. Birkett Foster's landscapes smile at one much in the same way that Mr. Carker used to flash his teeth, and Mr. John Collier gives his sitter a cheerful slap on the back before he says, like a shampooer in a Turkish bath, next man.

Applying Absorb-Decompose to orthogonalize the Attention Head introduces an equivalent transformation. If the near-zero singular values and their corresponding singular vectors are not removed, the model’s output remains completely unchanged.

Mr. Quilter is the apostle of the middle classes, and we are glad to welcome his gospel. 
Nor is Mr. Quilter's manner less interesting than his matter. 
He tells us that at this festive season of the year, with Christmas and roast beef looming before us, similes drawn from eating and its results occur most readily to the mind. 
He has grave doubts whether Sir Frederick Layton's work is really Greek after all, and can discover in it but little of rocky Ithaca. 
Linnell's pictures are a sort of Up Guards and Adam paintings, and Mason's exquisite idles are as national as a jingo poem. 
Mr. Birkett Foster's landscapes smile at one much in the same way that Mr. Carker used to flash his teeth, and Mr. John Collier gives his sitter a cheerful slap on the back before he says, like a shampooer in a Turkish bath, next man.

After applying the Absorb-Decompose method, we pruned singular values and their corresponding singular vectors with magnitudes close to zero ($S_{QK}\leq 5e^{-3}$ and $S_{VO}\leq 6e^{-3}$). This resulted in pruning ratios of 56.01% and 36.82% for the parameters in $W_Q$-$W_K$ and $W_V$-$W_O$, respectively. Remarkably, the model’s output remains nearly unchanged:

Mr. Quilter is the apostle of the middle classes, and we are glad to welcome his gospel. 
Nor is Mr. Quilter's manner less interesting than his matter. 
He tells us that at this festive season of the year, with Christmas and roast beef looming before us, similes drawn from eating and its results occur most readily to the mind. 
He has grave doubts whether Sir Frederick Layton's work is really Greek after all, and can discover in it but little of rocky Ithaca. 
Linnell's pictures are a sort of Up Guards and Adam paintings, and Mason's exquisite idles are as national as a jingo poem. 
Mr. Birkett Foster's landscapes smile at one much in the same way that Mr. Carker used to flash his teeth. And Mr. John Collier gives his sitter a cheerful slap on the back before he says, like a shampooer in a Turkish bath, next man.

In contrast, using a vanilla pruning method with the same pruning ratio, the model completely fails to produce valid outputs:

... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 

In fact, with Vanilla Pruning ratios of just 22.31% and 6.69% for $W_Q$-$W_K$ and $W_V$-$W_O$, respectively, the model’s output is already significantly degraded.

Mr. Colter is the personal of the classes, and we are glad to welcome his gospel. 
Nor is Mr. Colter's manner less interesting than his manner. 
He tells us that at this festive season of the year, with Christmas and roast beef looming before us, similarly he is drawn from eating and its results occur most readily to the mind. 
He is very dull, so very frequently, and is very Greek after all, and can discover in it but little of Rocky Ithaca. 
The Nell's pictures are sort of up-guard to Adam's paintings, and Mason's exquisite idylls are as national as a jingle poem. 
Mr. Burke and Foster's landscapes smile at one much in the same way as Mr. Parker, Mr. Flash is tits. And Mr. John Collier gives his sitter a cheerful slap on the back before he says like a shampoo and a Turkish bath, Next man.

This example validates our earlier statement that pruning a large number of non-zero dimensions accumulates loss, requiring fine-tuning to restore performance. In contrast, our Absorb-Decompose method losslessly consolidates parameters into a compact subspace, allowing the remaining directions to be freely pruned. By combining pruning with fine-tuning, training can be conducted with fewer resources directly within the latent space of the pre-trained model.

Absorb-Decompose for Fine-Tuning

In this section, we evaluate PESSA against Full-Parameter Fine-tuning, LoRA and DoRA on LLaMA-2-7B for commonsense reasoning tasks. We did not compare with SVFT due to its significant additional overhead. Commonsense reasoning tasks are divided into eight sub-tasks, detailed in Table 1. Following the DoRA setup, we fine-tune the combined Commonsense-170k dataset and evaluate the individual test set for each sub-task.

Table 1: Details of datasets being evaluated.

Dataset	# train	# test	About
BoolQ	9.4K	3,270	Naturally occurring yes/no questions from unconstrained settings.
PIQA	16.1K	1,830	Questions with two solutions requiring physical commonsense.
SIQA	33.4K	1,954	Reasoning about actions and social implications.
HellaSwag	39.9K	10,042	Commonsense NLI questions with context and endings.
WinoGrande	63.2K	1,267	Fill-in-the-blank task with binary options requiring commonsense reasoning.
ARC-e	1.1K	2,376	Grade-school multiple-choice science questions in Easy sets.
ARC-c	2.3K	1,172	Grade-school multiple-choice science questions in Challenge sets.
OBQA	5.0K	500	Questions requiring multi-step reasoning and commonsense knowledge.

For a fair comparison, we adopt the hyperparameter settings of DoRA (Table 2). The total number of trainable parameters in this setup is equivalent to fine-tuning $W_Q$, $W_K$, and $W_V$ using rank-$64$ LoRA.

Table 2. Detailed Training Hyperparameters. Q$^\dagger$ and K$^\dagger$ are derived by applying QR decomposition to $W_Q$ and $W_K$, while V$^\ddagger$ is obtained by applying SVD to $W_V$ and $W_O$. Only the upper triangular and diagonal matrices are fine-tuned, while orthogonal matrices remain frozen. 64$^\ast$ indicates that PESSA’s tunable parameters match LoRA with rank 64.

	Rank	Alpha	Dropout	LR	LR Scheduler	Batch size	Warmup Steps	Epochs	Target
LoRA	64	128	0.05	3e-4	Linear	16	100	3	Q,K,V
DoRA	64	128	0.05	2e-4	Linear	16	100	3	Q,K,V
PESSA	64$^\ast$	—	—	1e-4	Linear	16	100	3	Q$^\dagger$,K$^\dagger$,V$^\ddagger$

The experimental results of different methods are presented in Table 3. DoRA introduces a magnitude module, adding a small number of trainable parameters on top of LoRA, under the same rank. Additionally, as the dimension norm needs to be computed at every step, DoRA’s training speed is significantly slower than LoRA’s—approximately half the speed on a single A800 GPU we used. In contrast, PESSA only performs an initialization operation at the start of training, resulting in a training speed similar to LoRA. In this experiment, we did not prune redundant singular vectors. We believe that incorporating this training-free pruning technique could significantly reduce the number of frozen parameters, enabling more efficient training.

Table 3. Accuracy on eight commonsense reasoning tasks, with LLaMA-2-7B as the base model. bold indicates the highest accuracy.

Method	Params	BoolQ	PIQA	SIQA	HellaSwag	WinoGrande	ARC-e	ARC-c	OBQA	Avg.
LoRA	0.74%	70.9	81.3	79.3	87.8	80.3	80.6	66.0	80.0	78.3
DoRA	0.75%	71.1	82.4	78.1	90.2	81.4	82.7	68.5	80.0	79.3
PESSA	0.74%	74.3	85.7	81.1	94.4	85.9	88.4	74.9	84.6	83.7

From Table 3, our PESSA method significantly outperforms both LoRA and DoRA. For instance, PESSA achieves approximately 8% higher accuracy than LoRA and 6% higher than DoRA on ARC-easy and ARC-challenge tasks. On average, PESSA outperforms LoRA by 5.4% and DoRA by 4.4%. This notable improvement demonstrates the effectiveness of our approach, which fixes the orthogonal basis of the pre-trained model and learns its linear combinations.

Limitations

While Absorb-Decompose primarily supports Self-Attention, it also extends to Cross-Attention and cases where the input dimensions of $W_Q$ and $W_K$ differ, or the input dimension of $W_V$ differs from the output dimension of $W_O$. Additionally, it supports Causal Mask, Sliding Window mechanisms, and Linear layers with bias. However, the method currently does not support scenarios where nonlinear operations, such as ROPE or QK norm, exist between $W_Q$ and $W_K$. For these cases, we replace SVD with QR decomposition and directly decompose it by heads into an orthogonal matrix $Q$ and fine-tune the upper triangular matrix $R$.

Conclusion

In this paper, we highlight the importance of freezing the orthogonal basis and fine-tuning their linear combinations to improve the stability of pre-trained model fine-tuning. We analyze the trade-off between efficiency and stability in existing methods and propose the absorb-decompose operation to achieve a balance between the two. Which removes linearly dependent bases in attention heads, enabling training-free pruning of 46.42% of the parameters in the Whisper-large-v3 encoder attention. By fine-tuning a subset of singular values with moderate parameter counts and strong expressive power, our PESSA method outperforms LoRA by 5.4% on eight commonsense reasoning tasks. We believe this approach is valuable for both PEFT and pruning, while also providing insights into the attention mechanism and the fine-tuning process of large models.