Positional Embeddings in Transformer Models: Evolution from Text to Vision Domains

Positional encoding has become an essential element in transformer models, addressing their fundamental property of permutation invariance and allowing them to understand sequential relationships within data. This blog post examines positional encoding techniques, emphasizing their vital importance in traditional transformers and their use with 2D data in Vision Transformers (ViT). We explore two contemporary methods—ALiBi (Attention with Linear Biases) and RoPE (Rotary Position Embedding)—analyzing their unique approaches to tackling the challenge of sequence length extrapolation during inference, a significant issue for transformers. Additionally, we compare these methods' fundamental similarities and differences, assessing their impact on transformer performance across various fields. We also look into how interpolation strategies have been utilized to enhance the extrapolation capabilities of these methods; we conclude this blog with an empirical comparison of ALiBi and RoPE in Vision Transformers. To the best of our knowledge, this represents the first direct comparison of these positional encoding methods with those used in standard Vision Transformers.

Background

“Attention Is All You Need,” introduced by (Vaswani et al. [2017] ), revolutionized the field of natural language processing and computer vision by proposing a purely attention-based model, the Transformer, an efficient alternative for recurrent or convolutional networks.

Later, (Dosovitskiy et al. [2021] ) applied this concept to computer vision, introducing Vision Transformers (ViTs). On its own, the Transformer architecture is position-invariant, i.e., it processes its input as an unordered set. Unlike RNNs, designed to handle ordered sequences, or CNNs, which leverage translation equivariance and locality, transformers lack the inherent ability to capture sequential patterns. This is because the self-attention mechanism is independent of the token index.

(Vaswani et al. [2017] ) introduced positional encoding to address this lack of inductive bias. Since then, researchers have explored various methods to encode positional information directly into tokens or within the self-attention interaction step. The following sections will discuss the broad advancements of positional encoding methods in 1D and their extension for 2D tasks in Vision Transformers.

Preliminaries

Self-Attention Mechanism:

The self-attention mechanism processes sequences by representing each element as a vector of embedding dimension \(d\). For a sequence of length \(L\) and embedding dimension \(d\), the input is represented as a matrix \(X \in \mathbb{R}^{L \times d}\).

The mechanism employs three learnable weight matrices: \(W_Q,W_K,\) and \(W_V\) \(\in \mathbb{R}^{d \times d_{model}}\), where \(d_{model}\) represents the dimensionality of the projected subspaces. These matrices transform the input into queries, keys, and values respectively:

\[Q = X\,W_Q \;\;\;\;\;\;\;\; K = X \, W_K \;\;\;\;\;\;\;\; V = X \, W_V\]

The attention matrix is computed using the following formula:

\[\text{Attention}(Q, K) = \text{softmax}(QK^T/√d_{model})\] \[\mathbf{Z} = \text{Attention}(Q, K) \cdot V\]

With respect to each token, let \(x_i\) be the context vector for \(i^{\text{th}}\) token, the corresponding query, key and value vectors, \(\mathbf{q_i}, \mathbf{k_i}\) and \(\mathbf{v_i}\) are defined as follows:

\[\mathbf{q_i} = x_i \: W_Q \; \; \; \; \; \; \mathbf{k_i} = x_i \: W_K \; \; \; \; \; \; \mathbf{v_i} = x_i\:W_V\]

and \(N\) being total number of tokens , the attention score between the \(m_{th}\) token (query) and the \(n_{th}\) token (key) is formulated as

\[a_{m,n} = \frac{\exp\left( \frac{\mathbf{q}_m \mathbf{k}_n^\top}{\sqrt{d}} \right)}{\sum_{j=1}^{N} \exp\left( \frac{\mathbf{q}_m \mathbf{k}_j^\top}{\sqrt{d}} \right)}\]

and \(\mathbf{z}_m\) (output vector) for the \(m_{th}\) token is calculated as

\[\mathbf{z}_m = \sum_{n=1}^{N} a_{m,n} \mathbf{v}_n\]

Multi-Head Attention

In multi-head attention, the computation is extended across h parallel attention heads. Each \(head_i\) operates as:

\[\text{head}_i = \text{Attention}(Q\,W_Q^i, K\,W_K^i, V\,W_V^i)\]

The outputs from all heads are concatenated and projected back to the original dimensionality:

\[\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1,\ldots,\text{head}_h)\:W_O\]

where \(W_O \in \mathbb{R}^{hd_k \times d_{model}} , W_i^Q \in \mathbb{R}^{d_{\text{model}} \times d_k} , W_i^K \in \mathbb{R}^{d_{\text{model}} \times d_k}, \ W_i^V \in \mathbb{R}^{d_{\text{model}} \times d_k}, \ \text{and } W^O \in \mathbb{R}^{h d_k \times d_{\text{model}}}\) are learned matrices. Note \(d_{model} = h \times d_{k}\) and \(Q,K,V \in \mathbb{R}^{ L\times d_{\text{model}}}\)

Absolute Positional Embeddings

Absolute Positional embedding was introduced by (Vaswani et al. [2017] ) in their famous 2017 paper “Attention is All You Need”. It involves the direct addition of positional embeddings into the embedding vector. These encodings are injected only once in the embedding vector before passing them into the transformer block. Mathematically, it’s equivalent to 

\[x'_i := x_i + p_i\]

Where \(p_i\) is the positional embedding vector and \(x_i\) is the context vector corresponding to the \(i_{th}\) token. Note that \(x '_i,x_i ,p_i \in \mathbb{R}^d\). (Vaswani et al. [2017] ), proposed the following formula for \(p_i\)

\[\left\{ \begin{array}{ll} p_{i,2t} = \sin(i/10000^{2t/d}) & \\ p_{i,2t+1} = \cos(i/10000^{2t/d}) \\ \end{array} \right.\]

where \(p_{i,t}\) is the \(t^{th}\) element in the \(p_i\) vector.

Figure 1: Plot of sinusoidal positional embeddings, $i$ (position in sequence) vs $t$ (index in embedding vector). Each vertical strip can be seen as an absolute position embedding vector to be added.

One might question why a function of sines and cosines was chosen to represent positional encodings in a sequence—why not any other arbitrary function? The choice of sinusoidal functions was actually a strategic one, offering several advantages that benefit transformer models:

• Firstly the values are normalized between \([-1,1]\) allowing the model to learn parameters easily.
• The distance between neighboring positions is symmetrical and decays naturally with position.
• The formulation shows that every two consecutive elements in the embedding \(p_i\) share the same frequency denominator. For a pair with frequency \(w_k\), we can demonstrate that

\[\begin{array}{c}p_i \cdot p_{i+\phi} = \begin{bmatrix} \sin(iw_k) \\ \cos(iw_k) \end{bmatrix} \cdot \begin{bmatrix} \sin((i+\phi)w_k) \\ \cos((i+\phi)w_k) \end{bmatrix} \\[12pt] = \cos((i+\phi)w_k)\cos(iw_k) + \sin((i+\phi)w_k)\sin(iw_k) = \cos(\phi \: w_k)\end{array}\]

Hence the dot product \(p_i \cdot p_{i+\phi}\) is independent of position \(i\), and relative position \(\phi\) is retained. This consistency allows the model to capture regular intervals and patterns, making it especially effective for tasks requiring sequential dependencies.

The authors hypothesized that sinusoidal positional encoding would enable the model to learn relative positions naturally, thanks to the properties outlined above, and might also allow it to extrapolate to sequence lengths longer than those seen during training. This rationale led to sinusoidal positional embeddings being one of the first methods adopted in transformer architectures.

However, subsequent research challenged these assumptions. Studies found that absolute sinusoidal positional encoding was not well-suited for capturing relative positional information effectively (Shaw et al. [2018] ). Moreover, it struggled with extrapolation, leading to poor performance on sequence lengths longer than those encountered in training (Press et al. [2021] ).

Learned Positional Embeddings

In addition to sinusoidal positional embedding, (Vaswani et al. [2017] ) also explored learned positional encoding. They explored using a set of trainable vectors \(p \in \mathbb{R}^{L \times d}\) where \(L\) represents the maximum sequence length as positional embeddings. This method was applied in the (BERT [2018] ) and (GPT [2019] ) models as an alternative to sinusoidal positional encoding. However, it did not yield significant performance improvements over sinusoidal positional embedding. Moreover, the upper bound \(L\) limited the method’s ability to extrapolate to sequences longer than \(L\) without using interpolation techniques. Also, it introduces more trainable parameters, which increases the model’s size and computational cost.

Relative Positional Embeddings

Unlike absolute positional encodings, which create embeddings for each position independently, relative positional embeddings focus on capturing the pairwise relationships between tokens in a sequence. Also rather than directly adding the embeddings to the context vectors, the relative positional information is added to keys and values during the attention calculation. Hence

\[\mathbf{q_m} = x_m \:W_Q \; \; \; \; \; \; \mathbf{k_n'} = (x_n+ \tilde{p}_r^k)\:W_K\; \; \; \; \; \; \mathbf{v_n'} = (x_n+ \tilde{p}_r^v)\:W_V\]

where \(\tilde{\mathbf{p}}_r^k, \tilde{\mathbf{p}}_r^v \in \mathbb{R}^d\) are trainable relative positional embeddings and \(r = clip(m-n, Rmin, Rmax)\) represents the relative distance between the two tokens at positions $m$ and $n$. The maximum relative position is clipped, assuming a precise relative position is not useful beyond a certain distance. Further, clipping the maximum distance enables the model to extrapolate at inference time. However, this approach may not encode useful information about the absolute position of the token, which is useful in 2D tasks like Image Classification (Islam et al. [2019] )

Positional encoding in Vision Transformers

Motivated by the success of transformers in processing one-dimensional textual data, (Dosovitskiy et al. [2021] ) extended this approach to two-dimensional image data by introducing the Vision Transformer (ViT). In this work, they proposed a scalable transformer architecture with minimal adjustments to handle image data. The authors explored several approaches to positional embeddings for 2D images, including standard 1D learnable positional encoding based on the raster order of patches, spatially-aware 2D learned positional encoding and relative positional encoding. Their experiments revealed a significant performance gap between models without positional embeddings and those using any form of positional encoding. Interestingly, they observed little to no difference in performance between the different methods of encoding positional information. They speculated that because the transformer encoder operates on patch-level inputs rather than individual pixels, how spatial information is encoded becomes less critical; however, as will be seen subsequently in this blog, more advanced positional methods proposed for 1-dimensional data also lead to better performance in ViTs.

Rotary Positional Embeddings

Traditional positional encoding methods have primarily involved adding positional information directly to context embeddings. While this approach introduces a positional bias, it can limit the depth of interaction with attention weights, potentially underutilizing valuable relative position information. Additionally, since this information is added after the query-key multiplication, it does not contribute to the critical query-key similarity calculations that influence attention mechanisms.

Then came RoFormer (Su et al. [2021] ), which introduced a novel approach with Rotary Positional Embeddings (RoPE). Unlike conventional methods that add positional encodings to word embeddings, RoPE applies a rotary transformation to encode relative position information. This approach encodes relative position information without hindering the interaction of query-key pairs.

The mechanism of RoPE

Given the limitations of directly adding positional information, we need a formulation that encodes relative position information within the attention mechanism by applying a transformation solely to the query and key vectors.

Let token at position \(m\) has the context embeddings \(x_m\) , we define function \(f(x_m,m)\) which takes the context vector \(x_m\) and its position in the sequence \(m\) and returns a transformed embedding having the positional information. We want the function \(f\) to be such that the dot product of two embeddings depends on their relative position to each other i.e.

\[f(x_m,m)\cdot f(x_n,n) = g(x_m,x_n,m-n)\]

The two-dimensional case

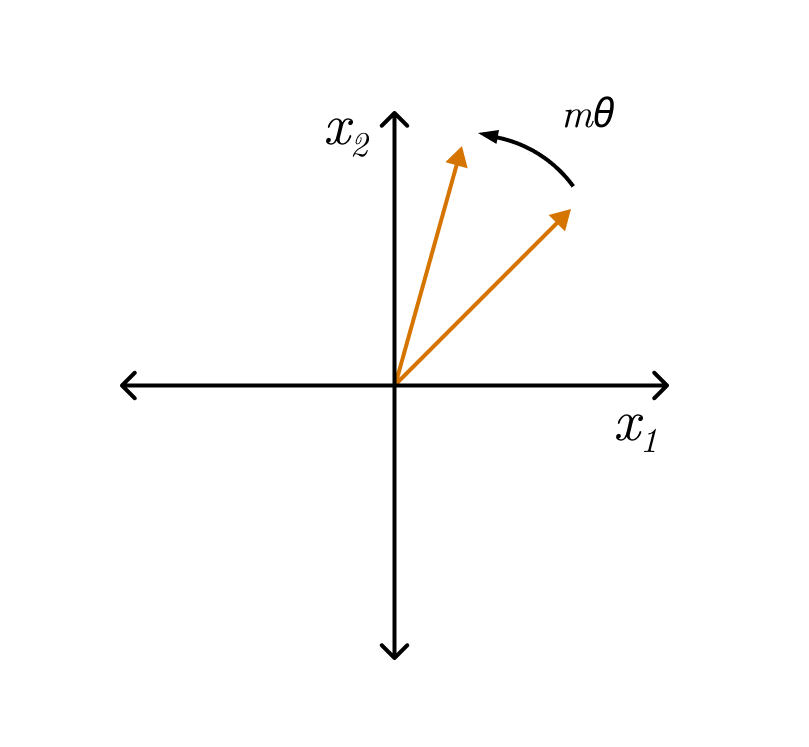
Consider the basic case where context vector \(x_m = \begin{pmatrix} x_m^{(1)} &x_m^{(2)}\end{pmatrix}^T\) is 2 dimensional and in complex space it can be represented as \(x_m^{(1)} + ix_m^{(2)}\) . For the exponential function, we know that \(e^m \cdot e^n = e^{m+n}\) which is very similar to the properties we want from the function \(f\). Thus for defining \(f\), we can multiply \(f\) \(x_m\) with \(e^m\) , but there is one problem that is explosion of magnitude as the sequence grows. Hence \(e^{im\theta}\) is an ideal choice for multiplication, as it doesn’t cause any magnitude changes and rotates the vector \(x_m\) by an angle of \(m\theta\).

\[f(x_m,m) = x_m e^{im \theta}\]

Formally, in order to encode the positional information, the key \(k_m\) at position \(m\) and query \(q_n\) at position \(n\) are multiplied with \(e^{im\theta}\) and \(e^{in\theta}\) respectively as a transformation. Consequently, the \((m,n)^{th}\) element of the attention matrix becomes -

\[q_n' = q_ne^{in \theta} \; \; k_m' = k_me^{in\theta}\] \[A'_{(n,m)} = \text{Re}[q^{'}_nk^{'*}_m] = \text{Re}[q_nk^*_me^{i(n−m)θ}] \;\;\;\;\;\;\;\;\;\;\;\; \scriptstyle \text{where Re[z] is the real part of z}\]

Hence the \(e^{i(n−m)θ}\) in this formulation of attention is responsible injecting relative position of the tokens which are \((n-m)\) distance apart from each other. The formal derivation that it is a solution to equation formulated is detailed in RoFormer (Su et al. [2021] ). Intuitively, we’re rotating 2D query and key vectors in the embedding space based on their sequence position. For example, the vector corresponding to first token is rotated by θ, the second by 2θ, and so on. The approach of rotating according to the position provides several benefits as discussed below -

Figure 2: Rotation of query, key vectors by $m\theta$ in 2D.

• Stability of Vectors: Adding tokens at the end of a sentence doesn’t affect the vectors for words at the beginning, facilitating efficient caching.
• Preservation of Relative Positions: If two words, say “pig” and “dog,” maintain the same relative distance in different contexts, their vectors are rotated by the same amount. This ensures that the angle, and consequently the dot product between these vectors, remains constant.

The general D-dimensional case

The idea of extending the 2D result to the d dimensional case is to break the embedding vector in various 2 dimensional chunks and rotate each one of them by a specific angle \(m\theta_i\) where m depends on the position of token in the sequence and \(\theta_i\) varies according to the chunk. This can be intuitively thought of as a corkscrew rotation in higher dimensions.

Figure 3: Visual representation of chunking of tokens and applying the rotation of different frequency $\theta_t$ on each chunk.

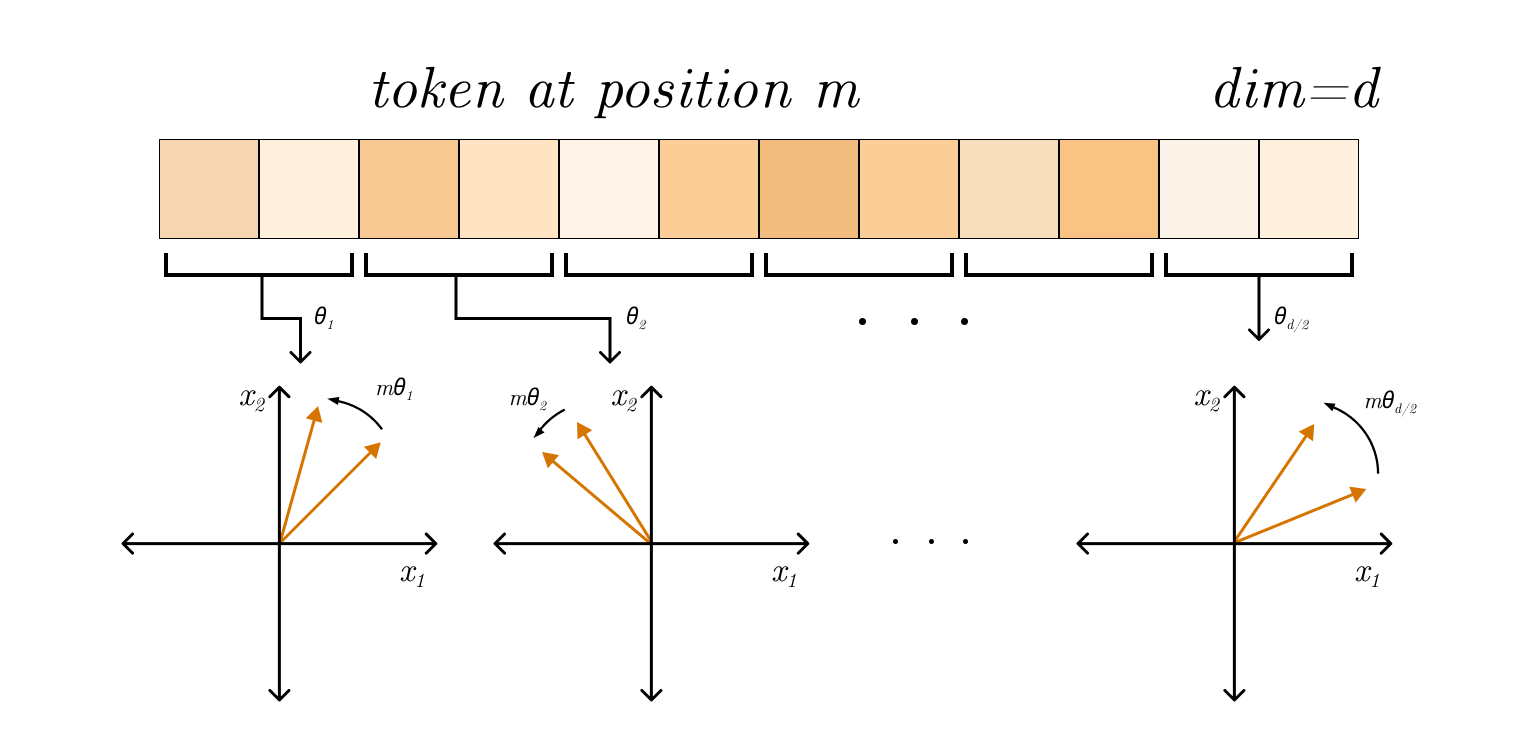
More formally, we divide the d dimensional space into smaller 2 dimensional subspaces, apply the rotation in those smaller subspaces and combine them again, this can be achieved through

\[q_n = R^{d}_{\Theta,n}\:W_q\:x_n, \; \; \; \;k_m = R^{d}_{\Theta,m}\:W_k\:x_m\]

where the transformation matrix \(R^{d}_{\Theta,m}\) is defined as follows -

\[R^{d}_{\Theta,m} = \begin{pmatrix} \cos m\theta_1 & -\sin m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ \sin m\theta_1 & \cos m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_2 & -\sin m\theta_2 & \cdots & 0 & 0 \\ 0 & 0 & \sin m\theta_2 & \cos m\theta_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2} & -\sin m\theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2} & \cos m\theta_{d/2} \end{pmatrix}\]

where the frequencies \(\theta_t\) are defined as follows -

\[\theta_t = 10000^{-t/(d/2)} \; \; \; \; \; t \in \{0,1, \cdots,d/2\}\]

This sums up the mathematical generalization for the d dimensional case of rotary positional embeddings. In order to make the notations simpler and easier to digest, we take an equivalent representation in complex space. Given the query and key vectors \(q_n, k_m \in \mathbb{R}^d\), we define complex vectors \(\bar{q_n}, \bar{k_m} \in \mathbb{C}^{d/2}\) by considering the \(2t^{th}\) dimension as real part and \(2t+1^{th}\) dimension as the complex part of the vector.

That is if \(q_n = (q^1_n,q^2_n,q^3_n,q^4_n, \cdots,q^{d-1}_n,q^d_n)\) then \(\bar{q_n} = (q^1_n+iq^2_n,q^3_n+iq^4_n, \cdots,q^{d-1}_n+iq^d_n) \in \mathbb{C}^{d/2}\) is its complex space counterpart, similar for key vectors. Now it can be proved that

\[q_nk_m^T = \operatorname{Re}[\bar{q_n} \bar{k_m}^T]\]

Using this idea of complex vectors, we can define a new transformation matrix \(\textbf{R} \in \mathbb{C}^{N \times (d/2)}\) as

\[\textbf{R}(n,t) = e^{i\theta_tn} \;\;\;\;\;\;\;\; \text{or} \;\;\;\;\;\;\;\;\textbf{R}(n) = \begin{pmatrix} e^{i\theta_1m} \\ e^{i\theta_2m} \\ \vdots \\ e^{i\theta_{d/2-1}m} \\ e^{i\theta_{d/2}m} \end{pmatrix}\]

and the transformation of RoPE can be reformed with Hadamard Product \(\circ\) as

\[\bar{q}' = \bar{q} \circ \textbf{R}, \; \; \; \; \bar{k}' = \bar{q} \circ \textbf{R}, \; \; \; \; \textbf{A}' = \operatorname{Re}(\bar{q_n} \bar{k_m}^T)\]

Where Hadamard product is the operation of taking element wise multiplication of corresponding matrices. We will be using this summarized notation to further define axial and mixed RoPE Positional Embeddings for ViT in later sections.

RoFormer (Su et al. [2021] ) has also shown that RoPE has long-term decay, meaning tokens with larger relative positional distances naturally exhibit weaker connections. This aligns intuitively with the idea that distant tokens should carry less influence on each other, improving context relevance. Additionally, RoPE enables linear self-attention models to incorporate relative positional embeddings, making it a versatile choice for efficient attention calculations. RoPE also enhances sequence length flexibility, allowing models to work with varying sequence lengths. However, RoPE’s extrapolation performance on sequence lengths much longer than those seen during training is somewhat limited.

RoPE in Vision Trasformers

(Heo et al. [2024] ) described various method to extend the idea of rotary positional embeddings to 2 dimensional application in Vision Transformers. Two approaches namely “Axial 2D Rope” and “RoPE Mixed” are discussed in the paper.

Axial 2D Rope

The core idea is to take and divide the embedding dimension into two and apply positional embedding for x-axis and y-axis separately, which is just repeating the 1d embedding twice. For indexing let patch positions in 2d image be \(\textbf{p}_n = (p_n^x, p_n^y)\) then the rotation matrix \(\textbf{R}\) from earlier section can be defined as

\[\textbf{R}(n,2t) = e^{i\theta_tp_n^x}, \; \; \; \; \textbf{R}(n,2t+1) = e^{i\theta_tp_n^y}\]

Hence we are interwining the rope along the two axes \(x\) and \(y\). As the range of indexes \((p_n^x, p_n^y)\) are reduced by square root, the RoPE frequencies \(\theta_t\) are also reduced by square root, i.e.

\[\theta_t = 100^{-t/(d/4)}, \;\;\;\;\;\text{where} \; t \in \{0,1,\cdots, d/4\}\]

Note that frequencies \(\theta_t\) for vision tasks are much larger than those used for language tasks. Also number of frequencies is halved so that \(d/2\) is covered by the contribution of both axes \(x,y\).

Mixed RoPE

The axial frequencies are unable to handle diagonal directions since frequencies only depend on either $x$ or $y$ axes. As the relative positions in RoPE are embedded in the form of \(e^{i\theta_t(n-m)}\) the relative positions are always interpreted as either \(e^{i\theta_t(p_n^x-p_m^x)}\) or \(e^{i\theta_t(p_n^x-p_m^x)}\), so the axial frequencies are not mixed in the axial direction.

In order to cater for mixed frequencies, the new rotation matrix \(\textbf{R}\) is proposed as

\[\textbf{R}(n,t) = e^{i(\theta_t^xp_n^x+\theta_t^yp_n^y)}\]

Unlike 1D RoPE and axial frequency RoPE, Mixed RoPE doesn’t define frequencies explicitly. Instead, it allows the network to learn frequencies \((\theta_t^x,\theta_t^y)\) for \(t \in \{0, 1, \cdots, d/2\}\) , as these are treated as learnable parameters. Separate sets of frequencies are used per head per self attention layer.

---

While RoPE tries to tackle the problems of Absolute and Learned positional encoding, another method that addresses this fundamental question in the realm of transformer models, i.e., “how to achieve extrapolation at inference time for sequences that are longer than those encountered during training,” is Alibi(Attention with linear bias) introduced by (Press et al. [2021] ).

Attention with Linear Biases (Alibi)

Unlike RoPE’s rotary approach, ALiBi introduces a novel mechanism for incorporating positional information into transformer models. The key innovation lies in its integration of positional encoding directly within the attention computation rather than at the token embedding level. This approach significantly differs from the previous one, focusing on relative positional relationships through a bias-based attention mechanism. One of ALiBi’s standout features is its complete removal of traditional positional embeddings at the input layer. Instead of adding positional encodings at the bottom of the network, ALiBi integrates them as biases within the attention layers themselves.

Mechanism and Architecture

ALiBi operates by injecting positional information through a bias matrix added to the self-attention scores before the softmax operation. The magnitude of this bias is proportional to the distance between the query and key tokens, establishing an intrinsic relationship between position and attention strength. Mathematically, this transforms the standard attention computation by introducing a position-aware bias term.

The architecture proposed by (Press et al. [2021] ) specifically addresses autoregressive decoder-only scenarios, implementing causal attention through a lower-triangular matrix structure. This ensures that each token can only attend to its predecessors. The resulting attention pattern can be represented as shown in the figure

Figure 4: Visualization of ALiBi's attention computation mechanism. The method introduces a head-specific linear bias matrix (right) that gets added element-wise to the standard query-key dot product attention scores (left). This bias injection occurs before the softmax operation, while preserving the remaining transformer architecture. The bias strength is controlled by a $m$, which is predetermined for each attention head.

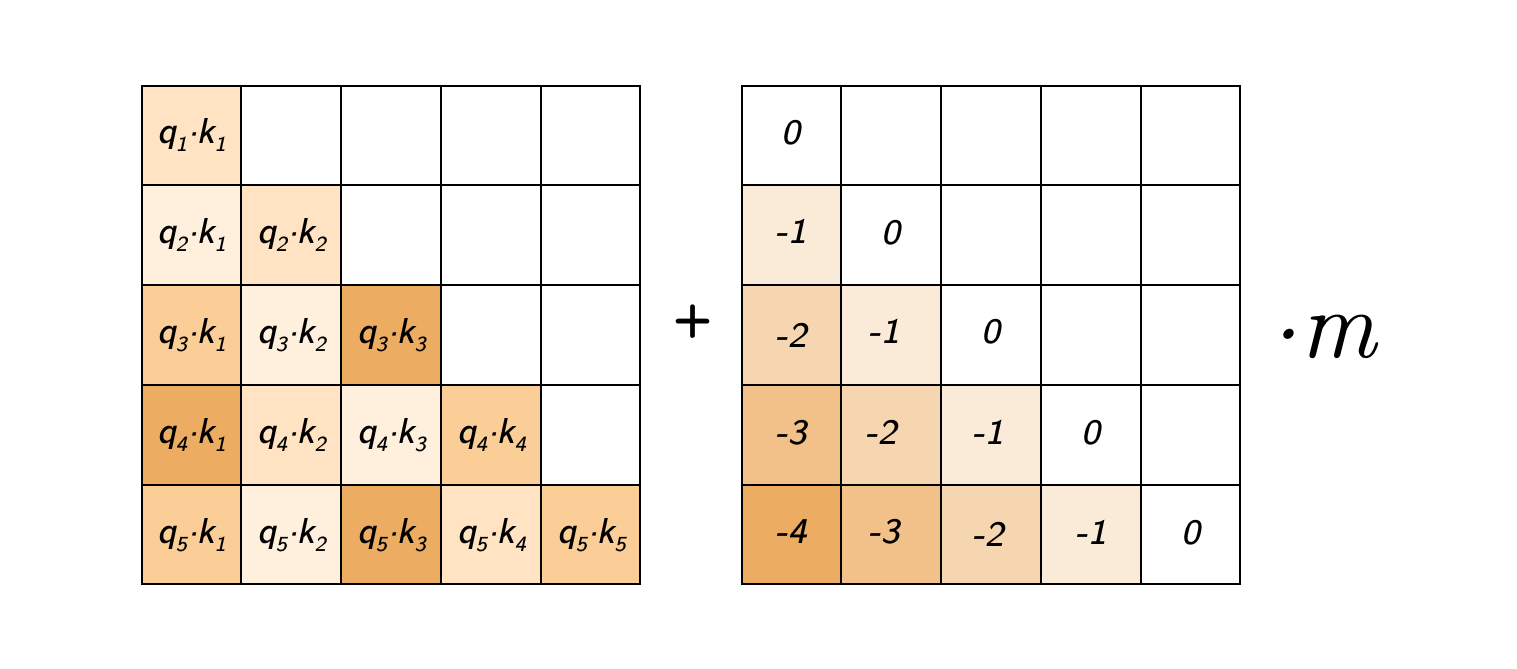
What is \(\textbf{m}\) ?

\(\textbf{m}\) is a non-learnable, head-specific slope parameter whose values follow a geometric sequence defined that starts at \(2^{-\frac{8}{n}}\) and uses that same value as its ratio, where \(n\) represents the number of attention heads.

This choice of slope values offers several benefits:

1. Diverse Temporal Scales: Each attention head is able to focus on different temporal scales, allowing the model to capture a range of positional relationships.
2. Ensemble Effect: The varied attention patterns create an ensemble-like effect, enriching the model’s representational power.
3. Contextual Flexibility: With slopes customized for different scales, the model can apply the most effective attention mechanisms for different contexts, adapting to both short and long-range dependencies.

Theoretical Foundation and Advantages

The core principle behind ALiBi lies in temporal relevance—a systematic adjustment of attention values based on the positional distance between queries and keys. This mechanism introduces an inductive recency bias, which has several advantages:

• Proportional Penalties: ALiBi applies penalties to attention scores based on the distance between tokens, with closer tokens receiving lower penalties and more attention.
• Enhanced Focus on Proximity: The method imposes stronger penalization on distant token relationships, naturally biasing the model toward more relevant, nearby tokens.
• Adaptive Penalization Across Heads: ALiBi allows each attention head to apply different penalty rates, enabling the model to capture both short-range and longer-range dependencies effectively.

Performance and Extrapolation

A standout feature of ALiBi is its remarkable ability to extrapolate to sequence lengths far beyond those seen during training. Unlike traditional positional encoding methods, ALiBi sustains robust performance even as sequence lengths grow significantly. This capability overcomes a fundamental limitation in standard transformer architectures, representing a major advancement in the scalability and adaptability of attention-based models.

Alibi in Vision Transformers

Building on ALiBi’s success with sequential data, researchers extended its application to two-dimensional image data in Vision Transformers (ViT). Translating ALiBi from 1D to 2D domains posed some challenges like adapting its causal attention mechanism for general self-attention and designing spatially aware 2D penalty metrics. These adjustments enabled ALiBi to effectively capture spatial dependencies in images, expanding what positional encoding can do in vision models.

Two-Dimensional Adaptation

The adaptation to 2D data, proposed by (Fuller et al. [2023] ), introduced several key modifications to the original ALiBi framework:

1. Symmetric Attention Structure: Unlike the lower triangular matrix in sequential processing, the 2D implementation employs a symmetric attention matrix, reflecting the bidirectional nature of spatial relationships in images.

2. Spatial Distance Metrics: The linear distance penalty is replaced by a Euclidean metric that captures 2D spatial relationships between image patches: \(\text{distance_penalty} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \cdot m\)

   where \(m\) retains its role as a non-learnable head-specific parameter.

Figure 5: Visualization of 2D ALiBi's attention computation mechanism.The bias matrix is now a symmetric matrix.

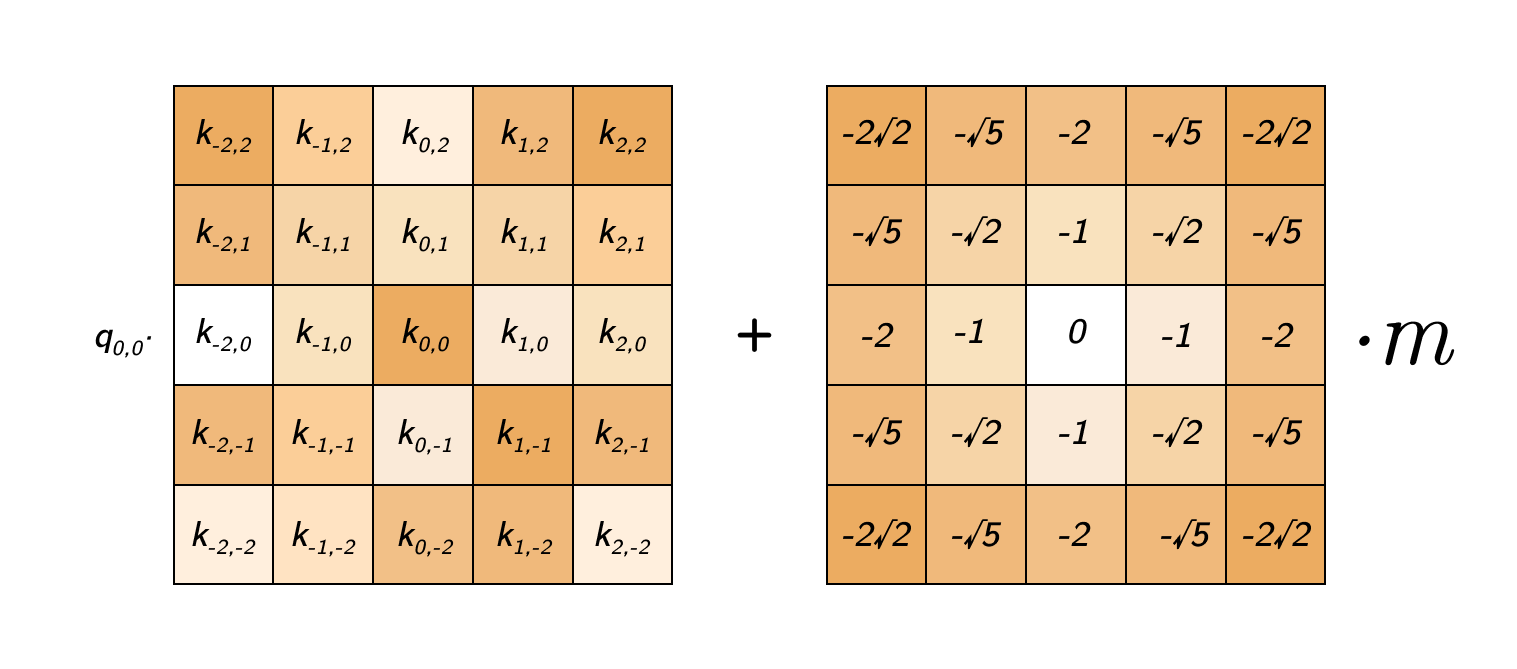
Comparative Analysis: RoPE and ALiBi

These two approaches, while sharing certain fundamental principles, represent distinct philosophical approaches to positional encoding:

Shared Characteristics

• Both RoPE and ALiBi on the principle of not adding positional encoding to word embedding, instead focusing on modifying the attention weights computed at every layer. This aligns with the thought that positional information and semantic information represent different things and that they should not be mixed.
• Both incorporate distance-dependent attention penalties. Both have an inductive recency bias and work on the philosophy that the farther a token is from a given token, the less relevant it is.

Key Distinctions

1. Mathematical Foundation
   • RoPE employs trigonometric transformations with theoretical guarantees. It uses the embedding vector’s rotation to capture positional information, while ALiBi utilizes straightforward linear distance penalties for encoding positional information.
2. Extrapolation Strength
   • Alibi demonstrates strong extrapolation capability, while RoPE struggles to extrapolate well enough above a number of tokens based on what it has been trained on.

Extrapolation via Interpolation

While ALiBi remains the only positional encoding method to demonstrate successful extrapolation to sequence lengths far beyond those encountered during training (Fuller et al. [2023] ), and has been adopted in models like MPT-7B (MosaicML NLP Team [2023] ), MPT-30B, BLOOM (Scao et al. [2023] ), and BloombergGPT (Wu et al. [2023] ), it hasn’t gained widespread traction. Many popular large language models (LLMs), like LLaMA (Touvron et al. [2023] ) and OPT (Zhang et al. [2022] ), still use Rotary Positional Embeddings (RoPE) or learned positional embeddings instead.

To address this challenge, (Chen et al. [2023] ) proposed a novel position interpolation approach to extend RoPE’s context window. They observed that directly extrapolating RoPE often led to exploding attention scores, which contradicts the expected recency bias inherent to RoPE. This issue arises because the theoretical upper bound proposed in RoFormer (Su et al. [2021] ) is loose, as (Chen et al. [2023] ) elaborate. To tackle this exploding attention score issue, they proposed interpolating sequences longer than the longest sequence encountered during training. Mathematically for a pre-trained LLM with a context window of size \(L\), we have the following formula for sequence of length \(L'\) with \(L'> L\) we have,

\[\mathbf{f}'(\mathbf{x}, m) = \mathbf{f} \left( \mathbf{x}, \frac{mL}{L'} \right) .\]

Here $f$ denotes the positional encoding function which takes the context vector $x$ and its position in the sequence $m$.

Thus, they reduce their position indices from \([0, L') \to [0, L)\)  to match the original range of indices before computing RoPE. Consequently, as inputs to RoPE, the maximum relative distance between any two tokens is reduced from \(L' \to L\). This alignment of ranges of position indices and relative distances before and after extension helps mitigate the effect on attention score computation due to context window extensions, which make the model easier to adapt.

Figure 6: An illustration of the Position Interpolation method in RoPE. Consider a LLM model pre-trained with a maximum sequence length of 2048. The upper left shows normal LLM usage where position indices stay within the pre-trained range. The upper right shows length extrapolation where models handle unseen positions up to 4096. The lower left shows Position Interpolation, where we downscale position indices from [0, 4096] to [0, 2048], keeping them in the pre-trained range.

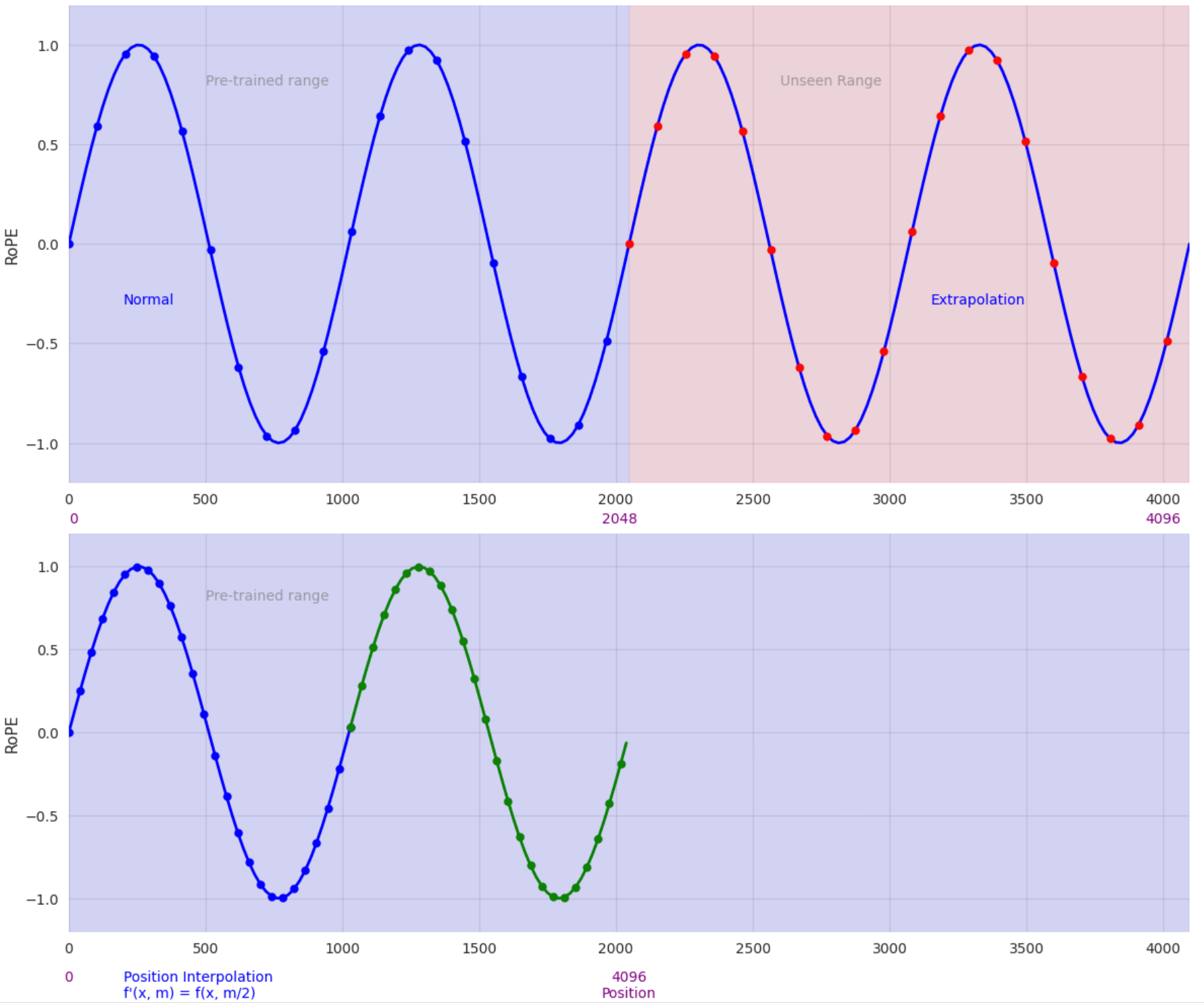
Recent research on extending the context windows of pre-trained Large Language Models (LLMs) has predominantly focused on position interpolation using RoFormer (Su et al. [2021] ) due to widespread use in many pre-trained LLMs. At the same time, the ALiBi positioning method has received comparatively less attention. A recent work by (Faisal Al-Khateeb et al. [2023] ) proposed an innovative approach to position interpolation for ALibi that significantly differs from (Chen et al. [2023] ) methodology. While (Chen et al’s. [2023] ) scaling operation was motivated by the problem of exploding attention score magnitudes during extrapolation, ALibi presents a different challenge: it generates lower magnitude attention scores for tokens in the extrapolation regime than the interpolation regime. To address this, (Faisal Al-Khateeb et al. [2023] ) introduced a dynamic slope scaling mechanism that adjusts the ALiBi slope to amplify attention scores, effectively preventing the decrease in magnitudes beyond the training context length. This approach involves scaling the slopes by a factor of \(L/L'\), where \(L\) represents the maximum sequence length during training and \(L'\) denotes the extended input sequence length during inference, expressed as \(m_j' = m_j(L/L')\). Importantly, this slope scaling is only applied when \(L'\) exceeds \(L\), ensuring the model maintains its original performance for sequences within the training length.

In the domain of computer vision, (Dosovitskiy et al. [2021] ), in their work on Vision Transformers, introduced a unique interpolation method to handle position embeddings during fine-tuning for higher-resolution images. Specifically, when adapting to higher resolutions, they maintained the original patch size, which increased the sequence length and caused pre-trained positional embeddings to lose spatial relevance. To address this, they applied 2D interpolation to the pre-trained position embeddings, preserving spatial relationships based on their original locations in the image. This approach differs from that of (Chen et al. [2023] ), who performed interpolation at the level of position indices rather than on the embeddings themselves. It also aligns more closely with (Faisal Al-Khateeb et al’s. [2023] ) rescaling technique, which similarly adjusts positional embeddings rather than rescaling indices for longer sequences.

Notably, the method proposed by (Faisal Al-Khateeb et al’s. [2023] ) required no additional training or fine-tuning. In contrast the approaches proposed by (Chen et al. [2023] ) and (Dosovitskiy et al. [2021] ) involved fine-tuning the model on longer sequences for effective extrapolation.

Experimental Evaluation

We conducted experiments comparing four architectural variants to empirically verify performance differences :

1. Standard Vision Transformer
2. Vision Transformer without positional encoding
3. Vision Transformer with 2D mixed-frequency RoPE
4. Vision Transformer with 2D ALiBi

Experimental Details

We trained all our models using the following hyperparameter scheme and high performance training recipes :

Hyperparameters	Value
Dataset	ImageNet100
Training Image Resolution	224x224
Number of Epochs	100
Number of Steps	50K
Number of Warmup Steps	10K
Warmup Schedule	Linear
Optimizer	AdamW
Base Learning Rate	1e-3
Learning Rate Schedule	Cosine Decay
Weight Decay	0.05
Optimizer Momentum	β1, β2 = 0.9, 0.999
Batch Size	256
RandAugment	(9, 0.5)
Mixup	0.8
Cutmix	1.0
Random Erasing	0.25
Label Smoothing	0.1

Initialisation Scheme:

CLS Token: Initialized using a standard normal distribution with mean 0 and variance 0.02 across all variants. The low variance prevents large initial values, reducing the risk of training instability.

Patch Embedding: We applied LeCun normal initialization for the convolutional patch embedding layer in all variants. Biases are initialized to 0, and weights use a truncated normal distribution based on input features.

Positional Embedding: For the standard Vision Transformer, the learned positional embedding in raster order are initialized with a standard normal distribution mean 0 and variance 0.02.

Classification Head: Both weights and biases in the final classification head are initialized to zero across all variants.

Multi-Head Attention Initialization: Attention layers use a uniform distribution, with bounds determined by the hidden dimension.

MLP Blocks and Layer Norms: Following PyTorch’s default initialization scheme:

• Linear layers use Kaiming uniform initialization.
• Layer normalization has weight initialized to 1 and bias to 0.

Results

Note: Values correspond to Top-1 validation set accuracy

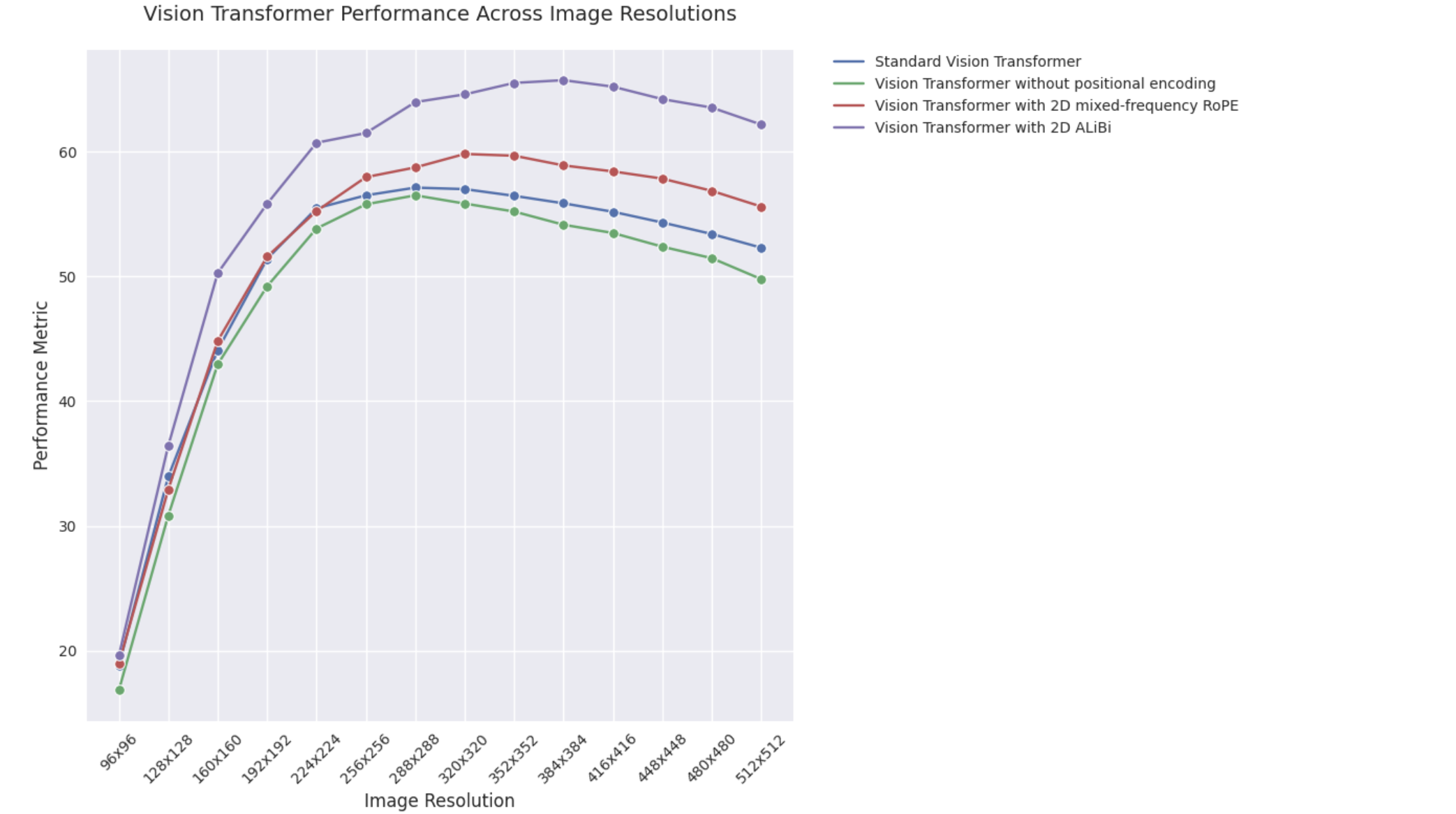
Resolution	Standard Vision Transformer	Vision Transformer without positional encoding	Vision Transformer with 2D mixed-frequency RoPE	Vision Transformer with 2D ALiBi
96x96	18.80	16.82	18.98	19.60
128x128	33.96	30.84	32.92	36.44
160x160	44.10	42.96	44.84	50.28
192x192	51.42	49.22	51.60	55.84
224x224	55.48	53.86	55.26	60.74
256x256	56.52	55.80	57.98	61.52
288x288	57.14	56.52	58.76	64.00
320x320	57.02	55.86	59.84	64.62
352x352	56.48	55.22	59.70	65.54
384x384	55.88	54.16	58.92	65.76
416x416	55.20	53.50	58.44	65.24
448x448	54.34	52.40	57.86	64.24
480x480	53.42	51.48	56.88	63.56
512x512	52.32	49.80	55.62	62.20

Note: Due to limited computational resources, we trained and evaluated our models on ImageNet100 https://www.kaggle.com/datasets/ambityga/imagenet100, a subset of ImageNet-1k. The subset comprises 100 classes with approximately 130,000 images for training and 5,000 images across 50 classes for validation. Additionally, we trained our model for 100 epochs instead of the standard 300 epochs commonly used for Vision Transformers (ViTs). Consequently, our results differ from those obtained on the full ImageNet-1k dataset. Our implementations of RoPE ViT and ALiBi are from their official github repos https://github.com/naver-ai/rope-vit,https://github.com/antofuller/CROMA respectively.

Further, we did not fine-tune the model on a higher sequence length. That is, all our results are for 0 shots. We extrapolated the standard Vision Transformer using 2D interpolation, whereas RoPE and Alibi did not require interpolation techniques as they can handle sequences of variable length. All models were trained using 2 T4 GPUs, with the following training times

Model	Training Time
Standard Vision Transformer	2 days 7 hours 47 minutes
Vision Transformer without positional encoding	2 days 8 hours 22 minutes
Vision Transformer with 2D mixed-frequency RoPE	2 days 10 hours 45 minutes
Vision Transformer with 2D ALiBi	2 days 8 hours 28 minutes

Key Findings

1. Both ALiBi and RoPE demonstrate superior extrapolation capabilities compared to the baseline ViT.
2. ALiBi exhibits better extrapolation performance over RoPE, similar to what has been observed in 1D data.
3. ALiBi also offers computational efficiency, reducing training time.

Conclusions

Our analysis of positional encoding mechanisms in Transformer architectures highlights several key insights:

1. The evolution of positional encoding and its fundamental role across diverse domains within Transformer architectures.
2. The sequence length extrapolation challenge, where RoPE and ALiBi demonstrate particular effectiveness in handling variable sequence lengths, especially ALiBi in extended contexts.
3. The adaptation of positional encoding from 1D to 2D tasks, with ALiBi showing practical advantages over RoPE in terms of computational efficiency and implementation simplicity.
4. The application of interpolation techniques to enhance the extrapolation capabilities of both RoPE and ALiBi positional encoding methods.
5. The empirical validation of RoPE and ALiBi positional encoding in standard Vision Transformers.