Repurposing in AI: A Distinct Approach or an Extension of Creative Problem Solving?

Creativity is defined as the ability to produce novel, useful, and surprising ideas. A sub area of creativity is creative problem solving, the capacity of an agent to discover novel and previously unseen ways to accomplish a task, according to its perspective. While creative problem solving has been extensively studied in AI, the related concept of repurposing - identifying and utilizing existing resources in innovative ways to address different problems from their intended purpose - has received less formal attention. This paper presents a theoretical framework that distinguishes repurposing from creative problem solving by formalizing both approaches in terms of conceptual spaces, resource properties, and goal achievement mechanisms. We demonstrate that while creative problem solving involves expanding the conceptual space through transformation functions, repurposing operates within existing conceptual spaces by leveraging shared properties of available resources. This formalization provides new insights into how these two approaches to problem-solving differ in their fundamental mechanisms while potentially complementing each other in practical applications.

In an era of rapid technological advancement and resource constraints, repurposing emerges as a crucial strategy for sustainable innovation and efficient problem-solving. The ability to adapt existing solutions to new goals promotes efficiency, allows us to maximize the utility of resources, reduce waste, and find novel solutions to complex problems. There are several notable use cases, from transforming industrial waste into valuable products to repurposing drugs for new medical treatments.

This blogpost aims at exploring the boundaries of creative problem solving (CPS) and proposes repurposing as a valid solution for those limitations. The section on CPS is based on . The original paper contains a wider overview of computational creativity and creative problem solving.

Creative Problem Solving

Creative Problem Solving is defined as the cognitive process of searching and coming up with creative and novel solutions to a given problem . This ability has proven to be non-trivial for systems, as it requires creativity, commonsense reasoning, and compositionality . In general, creative problem solving can be achieved through planning, learning, or hybrid methods.

Definition of Creative Problem Solving

We borrow and adapt the mathematical formalization from the creative problem solving framework proposed by and further developed by which follows the existing machine learning formalism.

In this framework, concepts are defined as either states of the environment or actions. \(C_X\) is the set of all concepts relating to \(X\), with \(X\) being environment states \(S\) and/or actions \(A\). In the creative problem solving framework, a goal \(G\) is unachievable if the conceptual space \(C_X\) is insufficient. To achieve the goal \(G\), the agent needs to discover a new conceptual space \(C_X' \not\subset C_X\) such that \(C_X' = f(C_X)\). Creative problem solving is the process of finding \(f\) to apply to the current conceptual space \(C_X\) to find \(C'_X\).

But what is a conceptual space? According to :

A “[conceptual space] is the generative system that underlies the domain and defines a certain range of possibilities: chess moves, or molecular structures, or jazz melodies. … in short, any reasonably disciplined way of thinking.”

Loosely speaking, the conceptual space of an agent is essentially its embedding space, that is to say, the space where the agent organizes data points to simplify how real-world data is represented.

The initial conceptual space known to the agent is not sufficient to reach the goal. Hence, CPS seeks to enable the agent to discover new concepts for accomplishing the goal by modifying the agent’s initial conceptual space into a new one.

Example:

We borrow the simplified example from illustrating a robot with the goal $G$ of transferring beans from a jar to a cooker: $G = in $(beans, cooker). The initial state is defined as $C_S = in$(beans, jar), $hasContainability$(spoon). The actions are defined as $C_A = scoop$(beans, $Z, loc_s, loc_d)$, where $Z$ refers to an object that satisfies $hasContainability(\cdot)$.

Per $C_S$, the agent doesn't know $hasContainability$(glass), for this reason the goal $G$ is un-achievable. In the creative problem-solving framework, when the robot doesn't have a spoon but has a glass, it uses a function $f(\cdot)$ to discover a new conceptual space: $f(C_S) = C'_S = C_S \cup \{hasContainability$(glass)$\}$, allowing it to solve the previously unsolvable task.

Repurposing

Repurposing is the process of adapting or transforming an existing concept, object, or solution to serve a new purpose or solve a different problem. At its core, repurposing is about seeing beyond the original intent and recognizing latent potential. It involves creative thinking to identify potential new uses for established ideas or resources, but the creative component is not always necessary.

Unlike creative problem-solving, which discovers new concepts, repurposing focuses on finding new ways to use existing resources within the current conceptual space. This process incorporates various aspects of creativity in the form of exploration of existing features of concepts.

Repurposing goes beyond simple reuse by requiring a systematic analysis of resource properties and their potential applications. While creative problem-solving expands the conceptual space through a function, repurposing works within by identifying how existing resources can be used differently based on their properties with the objective of making the most of our existing knowledge and resources.

Definition of Repurposing

Contrary to creative problem solving, repurposing does not involve expanding the conceptual space but rather involves finding new ways to use or interpret existing concepts within the current conceptual space \(C_X\) to achieve the goal \(G\). In other words, repurposing works within an existing conceptual space but changes the mapping between concepts based on their properties.

Let \(P\) be the set of all properties, and \(p: R → P\) be a property mapping function that identifies the properties of resources. Repurposing can be formally defined as a process that operates within:

• An existing conceptual space \(C_X\)
• A set of available resources \(R = {r_1, r_2, ..., r_n}\)
• A property mapping function \(p\) to achieve a goal \(G\).

Unlike creative problem solving, which expands the conceptual space, repurposing focuses on finding new mappings between existing resources based on their shared properties. Resources \(R\) are essentially instances or concrete realizations of concepts in \(C_X\).

The success of repurposing depends on three key factors:

1. The existing conceptual space \(C_X\)
2. The properties of available resources identified through \(p(R)\)
3. The adaptability (\(a\)) of the available resources \(R\), which quantifies how efficiently the existing resources can be repurposed to meet the new goal. It’s a measure of the flexibility of our resources and the efficiency of our repurposing solution. We define the adaptability score as: \(a = 1 - \frac{n}{N}\), where:

• $n$ is the number of resources that need to be replaced or added to achieve the repurposing goal
• $N$ is the total number of resources in the original concept
• a = 1 indicates perfect repurposing (using existing resources as-is)
• a = 0 indicates complete replacement (not really repurposing)

A higher adaptability score suggests a more efficient repurposing solution, as it requires fewer changes to the existing resources. This score helps us evaluate and compare different repurposing strategies, favoring those that make the most of what’s already available.

Repurposing works within the existing conceptual space by identifying and leveraging shared properties (P₁, P₂, P₃) among available concepts (c₁, c₂, c₃) to achieve goal G (whire requires property P₂).

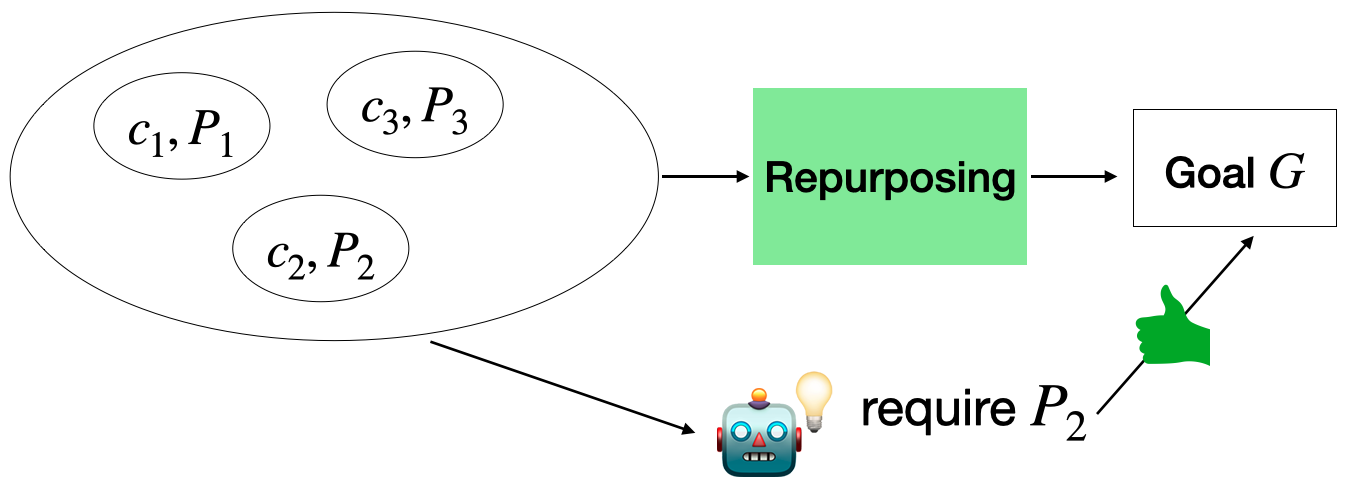
Therefore, repurposing finds a function \(g\) where: \(g: (C_X, R, p) → G\) where \(r\) is a new interpretation/mapping function that achieves \(G\) using the same \(C_X\) by leveraging the properties identified by \(p\).

Let us recall the previous example used to describe creative problem solving. For repurposing, the same example becomes:

Example:

Let's consider the same robot with the same goal of transferring beans from a jar to a cooker: $G = in $(beans, cooker). The initial state is defined as $C_S = in$(beans, jar), $hasContainability$(spoon). The actions are defined as $C_A = scoop$(beans, $Z, loc_s, loc_d)$, where $Z$ refers to an object that satisfies $hasContainability(\cdot)$. Let $P = \{$hasContainability, isTransparent$, ...\}$ be the set of properties for the resources available (in this case only the glass), and $R = \{$glass$\}$ be the set of available resources (no spoon available). The property mapping function $p$ reveals that $p$(glass) = $hasContainability$, indicating that the glass shares the crucial property needed for the scooping action.

In the repurposing framework, when the robot doesn't have a spoon but has a glass, it: (i) uses $p$ to identify that glass has the required containability property; (ii) maps the glass to fulfill the role of $X$ in the scoop action; (iii) achieves $G$ using the existing conceptual space $C_X = {C_S \cup C_A}$ and resource $R$ through $g(C_X, R, p)$.

This differs from creative problem solving which would expand \(C_S\) to include $hasContainability$(glass) as new knowledge. Instead, repurposing uses existing knowledge about properties to identify suitable resource substitutions within the current conceptual space.

Repurposing procedure

Successful repurposing requires a systematic approach to identify and leverage the properties of existing resources that could fulfill our goal requirements. The following procedure outlines how to analyze resources, map their properties, and assess their potential for repurposing, while maintaining the constraint of working within the existing conceptual space.

To determine how resources can be repurposed, we need to analyze their properties and potential transformations:

1. Property Mapping:
   • Define a property mapping function \(p: R \rightarrow P\)
   • For each resource \(r \in R\), identify its properties \(p(r)\)
   • Create a mapping of required properties for the goal \(G\)
2. Resource Analysis:
   • Compare properties of available resources \(p(r)\) with required properties for \(G\)
   • Identify resources that share properties with needed tools
   • Example: \(p\)(spoon) = \(\{\)hasContainability, hasHandle\(\}\) \(p\)(glass) = \(\{\)hasContainability, hasVolume\(\}\)
3. Compatibility Assessment:
   • Determine which resources can serve as substitutes based on shared properties
   • Identify any property gaps that might prevent repurposing
4. Transformation Requirements:
   • Count resources that need modification to achieve required properties
   • Identify any additional properties needed
5. Adaptability Score: \(a = 1 - n/N\) where:
   • \(N\) is the total number of original resources
   • \(n\) is the number of resources that needed property modifications

This framework emphasizes that repurposing relies on identifying and leveraging shared properties between resources, rather than discovering new properties (as in creative problem solving).

Solution Viability

The viability of a repurposing solution depends on how well it achieves the intended goal while utilizing existing resources and their properties. This assessment needs to consider multiple criteria, from the basic functionality to the practicality of the resource transformations. The evaluation must also account for how well the solution works within the constraints of the existing conceptual space \(C_X\).

To assess the effectiveness of repurposing, we introduce a task solvability function: \(S(G, C_X, R, p) = \frac{1}{|K|} \sum_{k \in K} w_k \cdot s_k(G, C_X, R, p)\) Where:

• \(K\) is the set of criteria that define goal satisfaction
• \(w_k\) is the weight of criterion \(k\) (with \(\sum_{k \in K} w_k = 1\))
• \(s_k(G, C_X, R, p)\) is the satisfaction score of criterion \(k\), ranging from 0 to 1
• \(p\) is the property mapping function that identifies resource capabilities

This function returns a value between 0 and 1, representing the degree to which the repurposing solution satisfies the goal criteria while working within the existing conceptual space and utilizing available resources.

Comparing Creative Problem-Solving and Repurposing

While both approaches aim to achieve the same goal, they differ fundamentally in how they utilize and transform available resources and conceptual spaces. Let’s consider the example of transforming the Spaghetti Bolognese dish into a low-carb version.

Creative Problem-Solving Framework

In this framework, we actively generate new concepts and properties through a transformation function f, allowing us to explore solutions beyond the limitations of our current conceptual space.

1. Define the Conceptual Space: Let \(C\) be the space of all possible dishes, where each dimension represents attributes like ingredients, cooking methods, flavors, textures, etc.

2. Initial Concept: \(c\) = Spaghetti Bolognese, represented as a point in \(C_X\)

3. Goal: \(G\) = Create a low-carb alternative

4. Creative Operators: We need to find a function f that expands the conceptual space: \(C'_X = f(C_X)\) where \(C'_X \notin C_X\)

5. Apply Transformation: The new solution \(c' ∈ C'_X\) = Zucchini Noodle Bolognese

6. Evaluate: Define a function \(E(c, G)\) that measures how well the new concept \(c'\) meets the goal \(G\). If \(E(c', G) > E(c, G)\), then the creative transformation is considered successful.

Repurposing Framework

On the other hand, repurposing focuses on finding new uses for existing resources within the current conceptual space. Unlike creative problem-solving, it emphasizes identifying and leveraging shared properties of resources to achieve goals without expanding the conceptual space itself.

1. Define the conceptual space and properties:
   • \(C_X = C_S ∪ C_A\) where:
     • \(C_S = \{\)pasta dish, Italian cuisine, high-carb meal\(\}\)
     • \(C_A = \{\)cook, prepare ingredients, serve\(\}\)

     Property mapping function \(p\) identifies:

     • \(p\)(pasta) = {\(hasCarbs, hasTexture\)}$$
     • \(p(\)vegetables) = {\(hasVolume, hasTexture\)}$$

2. Initial resources: \(R = \{\)pasta, ground beef, tomatoes, herbs, cooking equipment\(\}\) with their associated properties \(p(r)\) for each \(r \in R\)

3. Goal: \(G\) = Create a low-carb alternative

4. Repurposing Process:

   a. Identify resources with properties matching goal requirements

   b. Modify resource usage based on shared properties:

   • Reduce pasta quantity by 2/3
   • Use tomatoes’ hasVolume property to increase sauce, cooking them down to a thicker sauce
   • Leverage herbs’ flavor properties for satisfaction

5. Solution Implementation: Modified resource usage: \(R' =\){reduced pasta, ground beef, increased tomatoes, increased herbs, cooking equipment}

6. Evaluate Solution Viability: Calculate \(S(G, C_X, R, p)\) to assess goal satisfaction (Calculate adaptability score a = 1 - n/N post-hoc)

Using cooking as a testbed, we demonstrate the distinction between creative problem-solving and repurposing through interactions with GPT-4-turbo. We present two scenarios where the model is asked to solve cooking-related challenges. In the first scenario, with an open-ended prompt, the model typically suggests solutions involving new ingredients or tools, aligning with creative problem-solving. In the second scenario, when explicitly constrained to use only a specified set of available resources, the model shifts to repurposing-based solutions, finding innovative ways to use existing items. This observation highlights a key aspect of repurposing: the importance of clearly defining the resource set R and enforcing its constraints. Without explicit resource constraints, the model naturally defaults to creative problem-solving by expanding the conceptual space with new elements. To effectively elicit repurposing solutions, one must explicitly frame the problem in terms of a fixed set of available resources and their properties.

Differences and Advantages of Repurposing Framework

To summarize, here are the main differences between creative problem solving and repurposing:

1. Focus:
   • CPS: Primarily focused on generating novel solutions, which may or may not involve existing resources.
   • Repurposing: Specifically focused on finding new uses for existing resources or concepts.
2. Constraint consideration:
   • CPS: May consider constraints, but is not inherently bound by them.
   • Repurposing: Explicitly works within given resource constraints as a core principle.
3. Process:
   • CPS: May involve broader exploration of possibilities, including those outside current resources.
   • Repurposing: Starts with available resources and explores possibilities within that scope.
4. Applicability:
   • CPS: Useful in a wide range of scenarios, especially when novel solutions are needed.
   • Repurposing: Particularly valuable in resource-constrained or sustainability-focused contexts.

Some examples of the concepts defining creative problem solving and repurposing.

Discussion

While CPS is a powerful and essential approach in many scenarios, there are numerous problems that can benefit significantly from being framed as repurposing challenges. The dataset presented in provides an excellent example of such problems. The MACGYVER dataset, consisting of over 1,600 real-world problems designed to trigger innovative usage of objects and necessitate out-of-the-box thinking, can be viewed through the lens of repurposing rather than pure creativity. These problems often involve using existing objects or resources in novel ways to solve unexpected challenges - a hallmark of repurposing.

Framing these as repurposing problems offers several advantages:

• Property-Based Analysis: Repurposing explicitly considers the properties of available resources, helping identify non-obvious substitutions based on shared properties.
• Practical Feasibility: By focusing on actual properties of objects, the repurposing approach inherently considers the practicality of solutions, addressing the issue of physically-infeasible actions proposed by LLMs in the study.

By viewing such problems through the repurposing lens, we can potentially develop more effective strategies for AI systems. This approach complements creative problem solving, offering a structured method for innovation within constraints - a common scenario in real-world challenges.

Sample illustration from the MacGyver dataset . The problems in this dataset require innovative usage of objects among the ones available which is the scope of repurposing.

Conclusion

The exploration of repurposing through this mathematical framework has shed light on its relationship to creative problem-solving. While repurposing shares many characteristics with general creative problem-solving, our analysis reveals that it can be viewed as a specialized subset with distinct features:

• Constraint-Driven Creativity: Repurposing is inherently constrained by existing resources and structures, forcing creativity within defined boundaries.
• Efficiency Focus: Unlike open-ended creative problem-solving, repurposing emphasizes resource optimization and adaptability of existing solutions.
• Transformation Emphasis: While creative problem-solving can start from scratch, repurposing always begins with an existing concept or object, focusing on transformation and recontextualization.

These distinctions suggest that repurposing, while related to creative problem-solving, is a unique process that warrants specific attention and methodologies. Regarding the question of whether AI efforts should prioritize creative problem-solving over repurposing, our analysis suggests several compelling reasons to focus also on repurposing:

• Resource Efficiency: In a world of limited resources, repurposing offers a more sustainable approach to innovation.

• Structured Exploration: The constraints inherent in repurposing provide a more structured problem space for AI systems to explore, potentially leading to more practical and immediately applicable solutions.

• Cross-Domain Innovation: Repurposing encourages the transfer of ideas across different domains, a process that AI could potentially excel at by identifying non-obvious connections.

In conclusion, while repurposing and creative problem solving share common ground, repurposing emerges as a distinct and valuable approach. The structured nature of repurposing, combined with its focus on efficiency and transformation of existing solutions, makes it a particularly promising area for AI research and development. As we face increasingly complex global challenges, AI-driven repurposing could offer a powerful tool for innovation, potentially yielding more immediate and practical solutions than broader creative problem-solving approaches. Future work in this area could focus on developing AI systems that can effectively navigate the repurposing process. Additionally, further exploration of how humans and AI can collaborate in repurposing tasks could lead to powerful hybrid approaches, combining human intuition with AI’s vast knowledge and processing capabilities.