Gradient Similarity in Cnns A New Perspective on Class Concept Representation

Rethinking class similarity in deep learning models through the lens of gradient analysis. Our experiments on ResNet variants reveal that gradient-based similarity surpasses latent representation similarity in capturing class-level features, providing a fresh perspective on representation learning and model interpretability.

Introduction

In computer vision, understanding how models differentiate between classes has largely revolved around analyzing the latent representations and predicted probability distributions generated by these models. The conventional approach has been to treat the latent features as proxies for capturing the underlying similarities between different instances, which has become a cornerstone for representation learning, including self-supervised learning and knowledge distillation, as well as model interpretability. However, these representations are often influenced by various factors such as data augmentation and viewpoint changes, which can introduce inconsistencies in capturing true class-level invariant information from the final feature maps.

Observations

Our observation presented in this blog indicates that analyzing the gradient of a model’s prediction with respect to an input image provides a more consistent way to capture class concepts . Specifically, we observed that the gradients computed with respect to the maximum class prediction yield higher similarity across different instances of the same class compared to the latent representations and predicted scores alone. This observation suggests that gradients, which represent how changes in the input affect the model’s output, could serve as an important tool for understanding the true nature of class-specific invariant features and their role in the decision-making process.

The goal of this study is to propose a shift in the way we evaluate feature similarity and class representation in deep learning models. Instead of solely relying on the learned latent space, we argue that gradients computed with respect to specific class concepts can offer unique insights into how models internalize class-level invariant features. This approach not only allows us to better understand the latent representations but also provides a new avenue for model interpretability and representation learning by directly linking the gradients to the underlying class concept. To explore this hypothesis, we conducted experiments using generated datasets of ten animal classes and analyzed the similarity of gradients, latent representations, and predicted scores across various pre-trained ResNet architectures . Our results demonstrate that gradient-based similarity consistently outperforms traditional methods in capturing class-level invariant features, providing a compelling perspective for future use of gradient information as part of representation learning losses and the decision-making process.

Computing Gradient Weights of the Feature Map

To better understand how gradients can be leveraged for improved class representation, we first need to formally define how to compute gradient weights from the model’s intermediate feature maps . The concept of gradient weights allows us to assess the influence of each feature map channel on the final class prediction, and it forms the basis for our subsequent similarity analyses.

Consider a deep learning model $f(\mathbf{x}; \theta)$, where $\mathbf{x} \in \mathbb{R}^{H \times W \times C}$ is the input image and $\theta$ represents the model parameters. Let $\mathbf{F} \in \mathbb{R}^{C’ \times H’ \times W’}$ represent the feature map produced by an intermediate convolutional layer for the input image $\mathbf{x}$.

• Let $y_c$ be the predicted score for class $c$, where:

  \[y_c = f_c(\mathbf{x}; \theta)\]

  where $c = \arg\max(f(\mathbf{x}; \theta))$. In other words, $c$ is the index of the maximum predicted class.

• To calculate the gradient weights $\mathbf{w} \in \mathbb{R}^{C’}$, we take the gradient of $y_c$ with respect to the feature map $\mathbf{F}$:

  \[\mathbf{w}_k = \frac{1}{H' W'} \sum_{h=1}^{H'} \sum_{w=1}^{W'} \frac{\partial y_c}{\partial \mathbf{F}_{k, h, w}}, \quad \text{for } k = 1, 2, \ldots, C'\]

  Here, $\mathbf{w}_k$ represents the importance of the $k$-th channel of the feature map for the target class $c$, obtained by averaging the gradient over all spatial locations $(h, w)$. This averaging captures the global importance of each feature channel for the final class prediction, emphasizing which channels contribute most to the decision for the target class.

Cosine Similarity Computations

To quantify similarity between images using gradients and feature representations, we use cosine similarity . This metric measures the cosine of the angle between two vectors, reflecting their similarity in orientation regardless of magnitude.

The cosine similarity between two vectors $\mathbf{a}, \mathbf{b} \in \mathbb{R}^n$ is defined as:

\[\text{Cosine Similarity}(\mathbf{a}, \mathbf{b}) = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\| \|\mathbf{b}\|}\]

where $\mathbf{a} \cdot \mathbf{b}$ represents the dot product and $|\mathbf{a}|$ is the Euclidean norm.

• Feature Maps: For feature maps $\mathbf{F}_1, \mathbf{F}_2 \in \mathbb{R}^{C’ \times H’ \times W’}$, we flatten them into vectors:

  \[\mathbf{f}_1 = \text{flatten}(\mathbf{F}_1), \quad \mathbf{f}_2 = \text{flatten}(\mathbf{F}_2)\]

  The cosine similarity between these feature maps is:

  \[\text{Cosine Similarity}_{\text{FM}} = \frac{\mathbf{f}_1 \cdot \mathbf{f}_2}{\|\mathbf{f}_1\| \|\mathbf{f}_2\|}\]

• Final Predictions: For final prediction vectors $\mathbf{p}_1, \mathbf{p}_2 \in \mathbb{R}^K$, where $K$ is the number of classes:

  \[\text{Cosine Similarity}_{\text{P}} = \frac{\mathbf{p}_1 \cdot \mathbf{p}_2}{\|\mathbf{p}_1\| \|\mathbf{p}_2\|}\]

• Gradient Weights: For gradient weights $\mathbf{w}_1, \mathbf{w}_2 \in \mathbb{R}^{C’}$:

  \[\text{Cosine Similarity}_{\text{GW}} = \frac{\mathbf{w}_1 \cdot \mathbf{w}_2}{\|\mathbf{w}_1\| \|\mathbf{w}_2\|}\]

Experimental Protocol

To explore the effectiveness of gradient-based similarity. The protocol involved the following steps:

1. Data Generation:
   • We generated a dataset containing ten distinct animal classes using a Stable Diffusion Model . This allowed us to create diverse and realistic samples for each class, providing a rich dataset for evaluating similarities, while avoinding to test on samples which the pretained model is trained on.

Generated animal classes using stable diffusion.

1. CNN Architecture:
   • We utilized several ResNet variants ( ResNet-18, ResNet-34, ResNet-50, ResNet-101, ResNet-152).
   • For each generated image, we extracted three types of information: Latent Representations: (Extracted from the latent space of the final convolutional layer), Predicted Probability Scores: (The output scores for all classes), and the Gradients of Maximum Class Predicted (We consider the last Convolution layer).
2. Similarity Computation:
   • We computed the Cosine Similarity between all possible pairs of images on each class within the dataset for the three types of extracted information (latent representations, predicted scores, and gradient vectors).
   • Additionally, we computed the similarity of Grad-CAM maps using saliency metrics such as: Correlation Coefficient (CC), Similarity Metric (SIM), Kullback-Leibler Divergence (KLD), and Area Under the Curve (AUC) .

Illustration of overlaid GradCAM map on the generated snail classes using Resnet50.

1. Clustering Analysis:
   • We performed k-means clustering and Gaussian Mixture Model (GMM) clustering on each of the three extracted representations (latent, predicted scores, and gradients).
   • The quality of clustering was evaluated using the following metrics: Adjusted Rand Index (ARI), Normalized Mutual Information (NMI), and Silhouette Score
2. Evaluation:
   • We compared the performance of each type of representation (latent, predicted scores, gradients) across the similarity measures and clustering metrics.
   • The results were analyzed to determine which representation best captured the class-level similarities and yielded the most consistent clustering performance.

Expirmantal Results

Model\Matrices	‘Cos_Sim_GW’	‘Cos_Sim_P’	‘Cos_Sim_FM’	‘Grad_Cam_CC’	‘Grad_Cam_KLD’	‘Grad_Cam_SIM’	‘Grad_Cam_AUC’
Resnet18	0.832475	0.750405	0.809194	0.514107	0.546371	0.640893	0.473252
Resnet34	0.891979	0.760314	0.821133	0.547336	0.303619	0.717424	0.482986
Resnet50	0.970702	0.781508	0.842356	0.387207	0.845985	0.534813	0.441505
Resnet101	0.898816	0.777873	0.841248	0.451866	0.607102	0.587721	0.471974
Resnet152	0.918961	0.784820	0.834101	0.513276	0.560512	0.600739	0.498934

Where the columns of the table represent:

• Cos_Sim_G: Cosin similarity based on the gradiant.
• Cos_Sim_R: Cosin similarity based on the final represantations.
• Cos_Sim_act: Cosin similarity based on the activation map.
• Grad_Cam_CC: Grad_Cam accuracy.
• Grad_Cam_KLD: Grad_Cam Kullback–Leibler divergence.
• Grad_Cam_SIM: Grad_Cam Saliency similarity metric .
• Grad_Cam_AUC: Grad_Cam area under the curve.

Clustering using K-means

Models	Resnet18			Resnet34			Resnet50			Resnet101			Resnet152
Metric	ARI	NMI	Silhouette	ARI	NMI	Silhouette	ARI	NMI	Silhouette	ARI	NMI	Silhouette	ARI	NMI	Silhouette
Gradient Weights	0.95	0.98	0.79	0.63	0.85	0.62	1.00	1.00	0.89	0.95	0.98	0.83	0.77	0.91	0.81
Final Predictions	0.30	0.64	0.42	0.50	0.78	0.42	0.41	0.69	0.33	0.34	0.66	0.39	0.53	0.77	0.43
Feature Maps	0.41	0.72	0.42	0.57	0.80	0.51	0.41	0.73	0.49	0.23	0.57	0.41	0.39	0.69	0.35

Clustering using GMM

Models	Resnet18			Resnet34			Resnet50			Resnet101			Resnet152
Metric	ARI	NMI	Silhouette	ARI	NMI	Silhouette	ARI	NMI	Silhouette	ARI	NMI	Silhouette	ARI	NMI	Silhouette
Gradient Weights	0.95	0.98	0.79	0.61	0.85	0.62	1.00	1.00	0.89	0.95	0.98	0.83	0.77	0.91	0.81
Final Predictions	0.30	0.64	0.38	0.48	0.78	0.40	0.34	0.68	0.30	0.37	0.69	0.31	0.57	0.80	0.43
Feature Maps	0.46	0.74	0.42	0.52	0.77	0.48	0.41	0.73	0.49	0.24	0.58	0.39	0.40	0.71	0.30

Where the columns of the table represent:

• ARI: Adjusted Rand Index
• NMI: Normalized Mutual Information
• Silhouette: Silhouette score

Results Analysis

Quantitative Similarity Metrics

In terms of cosine similarity, the gradient weights consistently achieved higher values across all ResNet variants, with the highest value of 0.9707 observed for ResNet50. This indicates that the gradient-based representations capture a higher degree of similarity between images of the same class compared to the final predictions and feature maps. Specifically, the cosine similarity of final predictions (Cos_Sim_P) ranged from 0.7504 to 0.7848, while the cosine similarity of feature maps (Cos_Sim_FM) ranged from 0.8092 to 0.8424. These lower values suggest that the gradient weights are more effective in representing the underlying class relationships.

Regarding Grad-CAM metrics, the Grad-CAM Correlation Coefficient (Grad_Cam_CC) varied across ResNet variants, with ResNet34 achieving the highest value of 0.5473, reflecting the degree of alignment between Grad-CAM visualizations and the original class concepts. Grad-CAM KLD and SIM exhibited varying performance, with KLD reaching its lowest value for ResNet34 at 0.3036, suggesting minimal divergence between the Grad-CAM heatmaps and the target class. Grad-CAM AUC values were relatively consistent across the ResNet variants, indicating that Grad-CAM maps generally capture relevant features for class prediction, although not as distinctly as gradient weights.

Clustering Performance Analysis

For K-means clustering, gradient weights consistently outperformed the other representations across all ResNet variants. Specifically, for ResNet50, the ARI, NMI, and Silhouette scores were 1.00, 1.00, and 0.89, respectively, indicating near-perfect clustering alignment with the true labels. In contrast, the clustering performance of final predictions and feature maps was considerably lower. For ResNet50, final predictions achieved ARI, NMI, and Silhouette scores of 0.41, 0.69, and 0.33, while feature maps scored 0.41, 0.73, and 0.49. These findings indicate that final predictions and feature maps do not capture class-specific features as effectively as gradient weights.

A similar trend was observed for GMM clustering. The gradient weights again demonstrated superior clustering performance across all ResNet variants. For ResNet50, the ARI, NMI, and Silhouette scores were 1.00, 1.00, and 0.89, respectively, suggesting that gradient weights provide highly discriminative representations that align well with the true class labels. On the other hand, final predictions and feature maps showed weaker clustering performance, with ResNet50 scoring 0.34, 0.68, and 0.30 for ARI, NMI, and Silhouette, respectively, for final predictions, and 0.41, 0.73, and 0.49 for feature maps. These results reinforce the effectiveness of gradient-based representations for capturing class-level distinctions.

Plotting the gradient weights in comparison to the latent representations and the final prediction scores using PCA. The second and third rows represent the clustering results compared to the original classes, using KMeans and GMM, respectively.

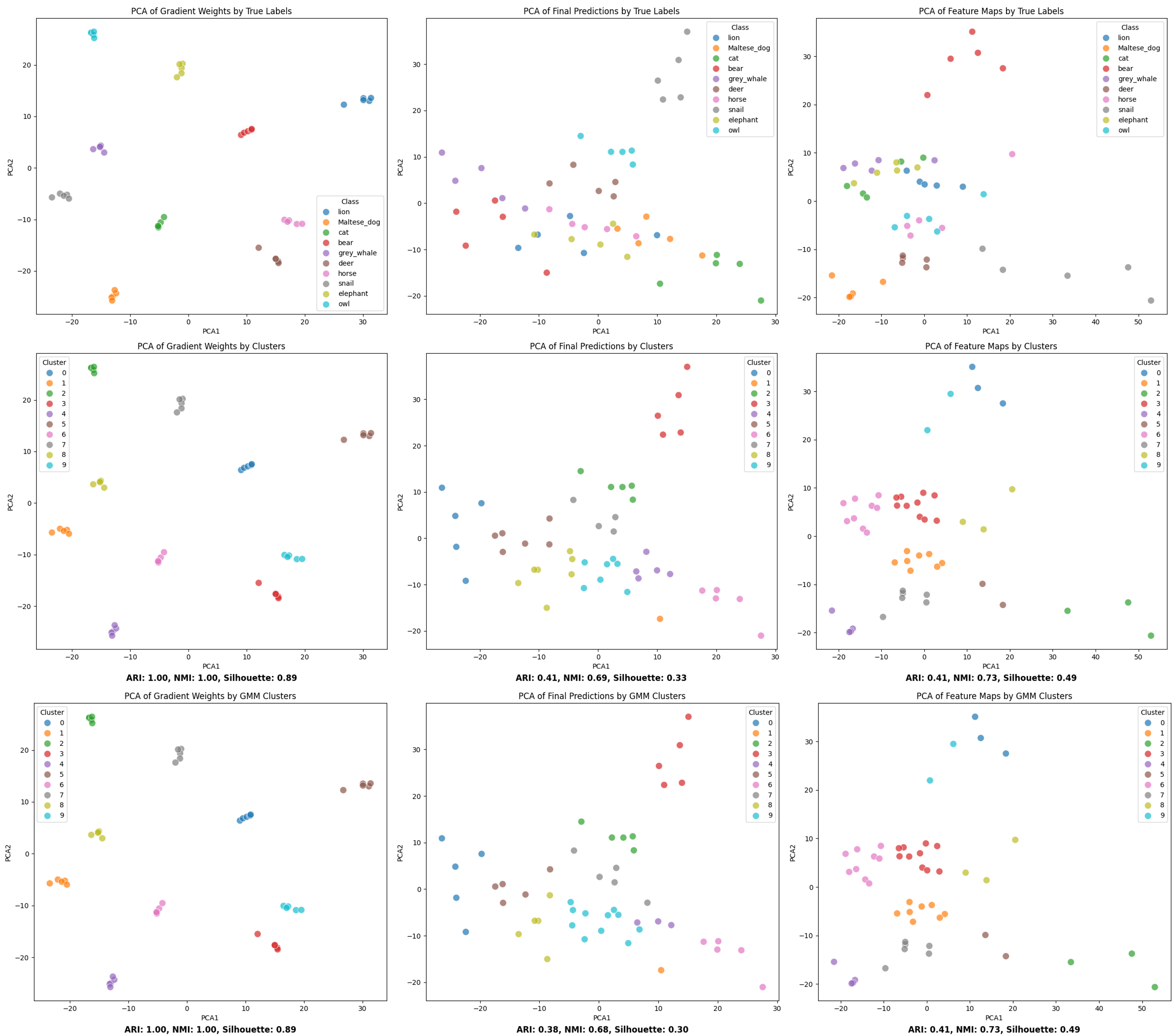
Qualitative Analysis of PCA Visualizations

The clustering performance of different representations was visualized using PCA on ResNet50 features to provide qualitative insights. The gradient weights formed distinct, well-separated clusters with minimal overlap, reflecting their effectiveness in capturing class-specific features, consistent with high ARI and NMI scores. In contrast, final predictions and feature maps showed significant overlap, indicating weaker class distinction. Both KMeans and GMM clustering methods yielded highly accurate results for gradient weights, while final predictions and feature maps had more scattered and overlapping clusters, leading to lower clustering performance metrics.

Key Insights

• Gradient-Based Representations consistently captured class-level information better than latent representations and predicted scores, as supported by both quantitative metrics and qualitative visualizations.

• PCA Visualizations showed that gradient weights formed distinct clusters with minimal overlap, while final predictions and feature maps had significant overlap, indicating lower discriminative power.

• Implications for Representation Learning Gradient analysis could be integrated into representation learning to improve model robustness and interpretability.

Conclusion and Future Directions

Our findings suggest that gradient-based similarity is a promising approach for capturing class-level information in deep learning models. Compared to traditional latent space representations and predicted probability distributions, the gradients computed with respect to the maximum class prediction provide a more consistent and measure of similarity between images of the same class. This observation holds across all ResNet variants evaluated on our generated dataset of animal images. Future work will explore the integration of these gradient-based metrics into training and their potential applications in advanced representation learning scenarios.